What Is The Critical Region In Statistics
Muz Play
Mar 31, 2025 · 7 min read
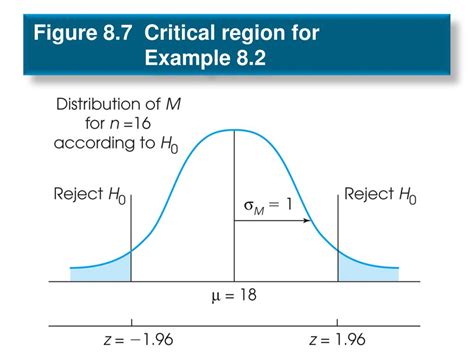
Table of Contents
- What Is The Critical Region In Statistics
- Table of Contents
- What is the Critical Region in Statistics? A Comprehensive Guide
- Understanding Hypothesis Testing
- What is the Critical Region?
- Defining the Boundaries of the Critical Region
- Visualizing the Critical Region
- Relationship with P-values
- Examples of Critical Regions in Different Tests
- 1. Z-test for a Population Mean
- 2. T-test for a Population Mean
- 3. Chi-Square Test
- 4. ANOVA (Analysis of Variance)
- Choosing the Right Significance Level (α)
- Importance of Understanding the Critical Region
- Beyond the Basics: Advanced Considerations
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
What is the Critical Region in Statistics? A Comprehensive Guide
Understanding statistical hypothesis testing is crucial for drawing meaningful conclusions from data. A core concept within this framework is the critical region, a concept often misunderstood but vital for accurate interpretation of results. This comprehensive guide will delve into the intricacies of the critical region, explaining its meaning, application, and significance in various statistical tests. We will explore its relationship with significance levels, p-values, and the overall decision-making process in hypothesis testing.
Understanding Hypothesis Testing
Before diving into the critical region, let's briefly review the fundamentals of hypothesis testing. The process typically involves:
-
Formulating Hypotheses: Defining a null hypothesis (H₀), representing the status quo or no effect, and an alternative hypothesis (H₁ or Hₐ), representing the effect we are trying to detect.
-
Setting a Significance Level (α): Determining the probability of rejecting the null hypothesis when it is actually true (Type I error). Common significance levels are 0.05 (5%) and 0.01 (1%).
-
Collecting Data: Gathering relevant data through experiments, surveys, or observations.
-
Calculating a Test Statistic: Computing a statistic that summarizes the data and reflects the difference between the observed data and what would be expected under the null hypothesis.
-
Determining the Critical Region: Identifying the range of values for the test statistic that would lead to the rejection of the null hypothesis.
-
Making a Decision: Comparing the calculated test statistic to the critical region. If the test statistic falls within the critical region, the null hypothesis is rejected; otherwise, it is not rejected.
What is the Critical Region?
The critical region, also known as the rejection region, is the set of values of the test statistic that leads to the rejection of the null hypothesis. It's essentially the area under the probability distribution curve that corresponds to the probability of observing the data given that the null hypothesis is true. If the calculated test statistic falls within this region, the results are considered statistically significant, meaning the observed data provides enough evidence to reject the null hypothesis in favor of the alternative hypothesis.
Defining the Boundaries of the Critical Region
The boundaries of the critical region are determined by the significance level (α) and the type of test (one-tailed or two-tailed).
-
One-tailed Test: In a one-tailed test, the critical region is located entirely in one tail of the distribution. This occurs when the alternative hypothesis specifies a directional change (e.g., "the mean is greater than X" or "the mean is less than X"). The critical region is either entirely in the upper tail (right-tailed test) or entirely in the lower tail (left-tailed test).
-
Two-tailed Test: In a two-tailed test, the critical region is split between both tails of the distribution. This occurs when the alternative hypothesis is non-directional (e.g., "the mean is different from X"). Each tail contains half of the significance level (α/2).
Visualizing the Critical Region
Imagine a normal distribution representing the sampling distribution of the test statistic under the null hypothesis. The critical region is visually represented by the area under the curve that lies beyond the critical values. These critical values are the boundaries separating the critical region from the non-critical region (acceptance region).
Relationship with P-values
While the critical region provides a clear boundary for decision-making, the p-value offers a more nuanced approach. The p-value represents the probability of obtaining results as extreme as, or more extreme than, the observed results, assuming the null hypothesis is true.
If the p-value is less than the significance level (α), it implies that the observed data falls within the critical region, leading to the rejection of the null hypothesis. Conversely, if the p-value is greater than or equal to α, the observed data falls within the acceptance region, and the null hypothesis is not rejected.
Examples of Critical Regions in Different Tests
The specific calculation and interpretation of the critical region vary depending on the statistical test used. Let's examine a few common examples:
1. Z-test for a Population Mean
In a Z-test, the critical region is determined using the standard normal distribution (Z-distribution). For a two-tailed test with α = 0.05, the critical values are approximately ±1.96. If the calculated Z-statistic falls outside this range (i.e., below -1.96 or above 1.96), the null hypothesis is rejected.
2. T-test for a Population Mean
Similar to the Z-test, the t-test utilizes the t-distribution to determine the critical region. The critical values depend on the degrees of freedom and the significance level. For a two-tailed test with α = 0.05 and 10 degrees of freedom, the critical values would be approximately ±2.228.
3. Chi-Square Test
The chi-square test is used for categorical data. The critical region in this test is determined using the chi-square distribution. The critical value depends on the degrees of freedom and the significance level. If the calculated chi-square statistic exceeds the critical value, the null hypothesis is rejected.
4. ANOVA (Analysis of Variance)
ANOVA tests for differences in means across multiple groups. The critical region is determined using the F-distribution. The critical value depends on the degrees of freedom for the between-group variance and the within-group variance, as well as the significance level.
Choosing the Right Significance Level (α)
The choice of the significance level (α) is a crucial aspect of hypothesis testing. A lower significance level (e.g., 0.01) makes it harder to reject the null hypothesis, reducing the chance of a Type I error (false positive). However, it also increases the risk of a Type II error (false negative), where a true effect is not detected. The selection of α often involves a trade-off between these two types of errors, considering the practical consequences of each.
Importance of Understanding the Critical Region
A robust understanding of the critical region is essential for proper interpretation of statistical results. It clarifies the decision-making process in hypothesis testing, providing a clear boundary between accepting and rejecting the null hypothesis. Misinterpreting the critical region can lead to incorrect conclusions and flawed decision-making based on statistical analyses.
Beyond the Basics: Advanced Considerations
While this guide provides a fundamental understanding of the critical region, several advanced considerations merit attention:
-
Power Analysis: Determining the sample size needed to achieve a desired level of power (the probability of correctly rejecting the null hypothesis when it is false) influences the critical region's size and sensitivity.
-
Effect Size: While statistical significance (determined by the critical region) indicates the presence of an effect, the effect size quantifies the magnitude of the effect. A statistically significant result might have a small effect size, indicating a limited practical importance.
-
Multiple Comparisons: When conducting multiple hypothesis tests simultaneously, the critical region needs adjustment to control for the inflated Type I error rate. Methods like Bonferroni correction are used to address this issue.
-
Non-parametric Tests: For data that doesn't meet the assumptions of parametric tests, non-parametric tests are employed. The critical region in these tests is determined using different probability distributions, such as the sign test or the Wilcoxon rank-sum test.
Conclusion
The critical region plays a fundamental role in statistical hypothesis testing. By understanding its definition, calculation, and interpretation, researchers can draw meaningful conclusions from their data. While the p-value offers a complementary approach, the critical region provides a clear visual and conceptual framework for decision-making. This comprehensive guide aims to equip readers with the knowledge to effectively utilize this critical concept in their statistical analyses. Remember that mastering statistical concepts takes practice and patience. Continuous learning and application are vital to building confidence and proficiency in statistical reasoning.
Latest Posts
Latest Posts
-
At Room Temperature The Various Conformations Of Butane
Apr 03, 2025
-
Scale Factor For The Circumference Of A Circle
Apr 03, 2025
-
Vertical And Horizontal Components Of A Vector
Apr 03, 2025
-
State Space Representation Of Transfer Function
Apr 03, 2025
-
Is Freezing Of Water A Chemical Change
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Is The Critical Region In Statistics . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
