Write In Standard Form The Equation Of Each Line
Muz Play
Apr 02, 2025 · 5 min read
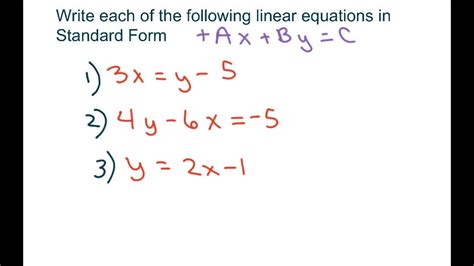
Table of Contents
Write in Standard Form the Equation of Each Line: A Comprehensive Guide
The standard form of a linear equation is a fundamental concept in algebra and geometry. Mastering it is crucial for understanding lines, their properties, and their relationships with other geometric figures. This comprehensive guide will walk you through various methods of writing the equation of a line in standard form, covering diverse scenarios and providing ample examples to solidify your understanding.
What is the Standard Form of a Linear Equation?
The standard form of a linear equation is expressed as Ax + By = C, where:
- A, B, and C are integers (whole numbers, positive, negative, or zero).
- A is non-negative (A ≥ 0). This convention ensures consistency.
- A, B, and C are usually written as the smallest possible integers, representing the simplest form of the equation. This is achieved through simplification and reduction.
This form offers a structured and consistent way to represent any straight line on a coordinate plane. It provides readily available information about the line, such as its intercepts (x and y) and slope.
Methods to Write the Equation of a Line in Standard Form
Several methods exist for deriving the standard form equation, depending on the information given. Let's explore the most common ones:
1. Using Slope-Intercept Form (y = mx + b)
The slope-intercept form, where 'm' represents the slope and 'b' the y-intercept, is a convenient starting point. To convert this form into the standard form, follow these steps:
- Rearrange the equation: Move the 'mx' term to the left side of the equation. This yields -mx + y = b.
- Make A non-negative: If 'm' (or 'A') is negative, multiply the entire equation by -1 to make 'A' positive.
- Ensure integers: Multiply the entire equation by an appropriate integer to eliminate fractions or decimals and express all coefficients as whole numbers.
Example: Convert y = 2/3x + 4 into standard form.
- -2/3x + y = 4
- Multiply by 3 to eliminate the fraction: -2x + 3y = 12
Therefore, the standard form is 2x - 3y = -12.
2. Using Point-Slope Form (y - y1 = m(x - x1))
The point-slope form uses the slope 'm' and a point (x1, y1) on the line. Here's the conversion process:
- Expand the equation: Distribute 'm' to both terms inside the parentheses. This gives y - y1 = mx - mx1.
- Rearrange: Move the 'mx' term and 'y1' term to the left side, resulting in -mx + y = y1 - mx1.
- Adjust for standard form: Ensure 'A' is non-negative and all coefficients are integers.
Example: Find the standard form equation for a line with slope 2 passing through the point (1, 3).
- y - 3 = 2(x - 1)
- y - 3 = 2x - 2
- -2x + y = 1
The standard form is 2x - y = -1.
3. Using Two Points (x1, y1) and (x2, y2)
When given two points on a line, we first need to find the slope before using the point-slope form.
- Calculate the slope (m): m = (y2 - y1) / (x2 - x1)
- Use the point-slope form: Substitute the slope 'm' and one of the points (x1, y1) into the point-slope form.
- Convert to standard form: Follow steps 2 and 3 from the previous section.
Example: Find the standard form for a line passing through points (2, 1) and (4, 5).
- m = (5 - 1) / (4 - 2) = 4 / 2 = 2
- Using point (2, 1): y - 1 = 2(x - 2)
- y - 1 = 2x - 4
- -2x + y = -3
- 2x - y = 3
4. Using Intercepts (x-intercept and y-intercept)
The x-intercept is the point where the line crosses the x-axis (y = 0), and the y-intercept is where it crosses the y-axis (x = 0).
- Identify intercepts: Let (a, 0) be the x-intercept and (0, b) be the y-intercept.
- Use the intercept form: The equation of a line in intercept form is x/a + y/b = 1.
- Convert to standard form: Multiply the entire equation by 'ab' to eliminate fractions. Then rearrange to match Ax + By = C.
Example: Find the standard form for a line with x-intercept 3 and y-intercept 2.
- x/3 + y/2 = 1
- Multiply by 6: 2x + 3y = 6
The standard form is 2x + 3y = 6.
Special Cases: Horizontal and Vertical Lines
Horizontal and vertical lines require specific attention.
Horizontal Lines
A horizontal line has a slope of zero (m = 0). Its equation is simply y = b, where 'b' is the y-intercept. The standard form is 0x + 1y = b (or simply y = b).
Vertical Lines
A vertical line has an undefined slope. Its equation is x = a, where 'a' is the x-intercept. The standard form is 1x + 0y = a (or simply x = a).
Applications of Standard Form
The standard form is valuable in various contexts:
- Determining intercepts: The x-intercept is found by setting y = 0 and solving for x; the y-intercept is found by setting x = 0 and solving for y.
- Graphing lines: Finding the intercepts provides two points to plot and draw the line.
- Solving systems of equations: The standard form simplifies the process of using elimination or substitution methods to find the intersection point of two lines.
- Representing constraints: In linear programming, standard form is essential for defining constraints and optimizing objectives.
Practice Problems
Let's test your understanding with a few practice problems:
-
Write in standard form the equation of a line with slope -1/2 and passing through the point (-2, 4).
-
Write the standard form equation of a line passing through points (1, -3) and (4, 0).
-
Convert y = -3x + 5 into standard form.
-
Find the standard form of the equation for a line with x-intercept -2 and y-intercept 5.
-
What is the standard form equation of a horizontal line passing through the point (3, -2)?
-
Write the standard form of a vertical line passing through (5, 1).
Solutions:
- x + 2y = 6
- 3x - y = 6
- 3x + y = 5
- 5x - 2y = -10
- y = -2
- x = 5
By practicing these methods and solving various problems, you will build a strong foundation in understanding and utilizing the standard form of linear equations. Remember, mastering this concept is essential for progressing in higher-level mathematics and related fields. Consistent practice and a clear understanding of the principles are key to success.
Latest Posts
Latest Posts
-
Heat Of Vaporization Of Water J Kg
Apr 03, 2025
-
What Happens To Plant Cells In A Hypertonic Solution
Apr 03, 2025
-
What Is A Disadvantage Of A Corporation
Apr 03, 2025
-
What Is Kf In Freezing Point Depression
Apr 03, 2025
-
What Are Some Disadvantages Of A Corporation
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Write In Standard Form The Equation Of Each Line . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
