Writing Geometric Series In Summation Notation
Muz Play
Mar 26, 2025 · 5 min read
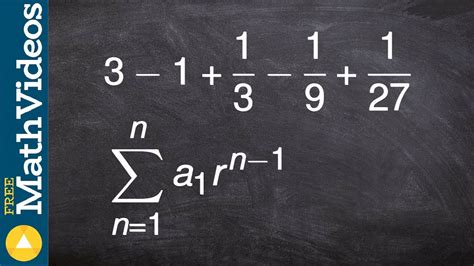
Table of Contents
Writing Geometric Series in Summation Notation: A Comprehensive Guide
Geometric series are a fundamental concept in mathematics with widespread applications in various fields, from finance and engineering to computer science and physics. Understanding how to represent these series using summation notation is crucial for manipulating and analyzing them effectively. This comprehensive guide will delve into the intricacies of writing geometric series in summation notation, providing a clear and detailed explanation suitable for students and professionals alike.
What is a Geometric Series?
A geometric series is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio, often denoted by 'r'. The first term is denoted by 'a'. Therefore, a geometric series can be represented as:
a, ar, ar², ar³, ar⁴, ...
Key characteristics of a geometric series:
- Constant Ratio: The ratio between consecutive terms remains constant throughout the series.
- First Term: The initial term of the series is denoted by 'a'.
- Common Ratio: The constant multiplier between consecutive terms is denoted by 'r'.
Summation Notation: A Powerful Tool
Summation notation, also known as sigma notation (Σ), provides a concise way to represent the sum of a series. It uses the Greek capital letter sigma (Σ) to indicate summation. The general form of summation notation is:
Σ_{i=m}^{n} f(i)
Where:
- Σ: Represents the summation symbol.
- i: Is the index of summation (a counter variable).
- m: Is the lower limit of summation (the starting value of i).
- n: Is the upper limit of summation (the ending value of i).
- f(i): Is the expression to be summed. Each term in the series is obtained by substituting the current value of 'i' into f(i).
Expressing Geometric Series in Summation Notation
To represent a geometric series using summation notation, we need to identify the first term ('a'), the common ratio ('r'), and the number of terms ('n'). The general formula for the nth term of a geometric series is:
ar^(n-1)
Therefore, a finite geometric series with 'n' terms can be written in summation notation as:
Σ_{i=1}^{n} ar^(i-1)
Explanation:
- Σ_{i=1}^{n}: This indicates that we are summing from i = 1 to i = n.
- ar^(i-1): This is the general term of the geometric series. As 'i' increases from 1 to n, we generate each term of the series: a, ar, ar², ar³, ..., ar^(n-1).
Example 1: A Simple Geometric Series
Let's consider the geometric series: 2, 6, 18, 54, 162.
Here, a = 2 and r = 3 (since 6/2 = 3, 18/6 = 3, and so on). There are 5 terms, so n = 5. Therefore, the summation notation is:
Σ_{i=1}^{5} 2 * 3^(i-1)
Example 2: A Geometric Series with a Negative Common Ratio
Consider the series: 1, -2, 4, -8, 16.
Here, a = 1 and r = -2. With n = 5 terms, the summation notation becomes:
Σ_{i=1}^{5} 1 * (-2)^(i-1)
Example 3: A Geometric Series Starting from a Different Index
While the index typically starts at 1, it can start from any integer. Consider the series: 4, 12, 36, 108. This is a geometric series with a = 4 and r = 3. If we want to represent it using summation notation starting from i=0, we'd adjust the exponent accordingly:
Σ_{i=0}^{3} 4 * 3^i
Infinite Geometric Series
For infinite geometric series (where the number of terms approaches infinity), the summation notation remains largely the same, but the upper limit becomes ∞:
Σ_{i=1}^{∞} ar^(i-1)
However, an infinite geometric series only converges (has a finite sum) if the absolute value of the common ratio |r| is less than 1 (|r| < 1). If |r| ≥ 1, the series diverges (its sum approaches infinity).
The sum of a convergent infinite geometric series is given by the formula:
S = a / (1 - r)
This formula is extremely useful for various applications.
Applications of Geometric Series
Geometric series find numerous applications across diverse fields:
- Finance: Calculating compound interest, annuities, and loan repayments.
- Physics: Modeling exponential decay (e.g., radioactive decay) and oscillatory motion.
- Computer Science: Analyzing algorithms and data structures, especially those involving recursive processes.
- Engineering: Analyzing signal processing and control systems.
- Probability: Calculating probabilities in scenarios with repeated independent trials (e.g., coin flips).
Advanced Topics and Considerations
- Nested Summations: Geometric series can be combined with other series, leading to nested summations. These require careful evaluation, often involving changing the order of summation.
- Partial Sums: Analyzing partial sums (sums of a finite number of terms) of a geometric series provides insights into the convergence behavior of the infinite series.
- Relationship to Other Series: Understanding the connections between geometric series and other types of series (like arithmetic series or power series) expands your mathematical toolkit.
Conclusion: Mastering Summation Notation for Geometric Series
Writing geometric series in summation notation is a crucial skill for anyone working with sequences and series. By understanding the fundamental principles and applying the formulas correctly, you can efficiently represent, analyze, and manipulate these powerful mathematical tools. This guide has provided a thorough overview of the key concepts, examples, and applications, equipping you with the knowledge to tackle a wide range of problems involving geometric series. Remember to practice regularly, explore advanced topics, and apply this knowledge to real-world scenarios to deepen your understanding and build a strong foundation in mathematics. This will empower you to solve complex problems and contribute effectively to your chosen field.
Latest Posts
Latest Posts
-
The Number Of Electrons Moving Is Known As
Mar 29, 2025
-
Increasing The Pressure Of A Gas Solution Will
Mar 29, 2025
-
How Many Pi Electrons In A Double Bond
Mar 29, 2025
-
Political Effects Of The Industrial Revolution
Mar 29, 2025
-
Ground State Electron Configuration For C
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Writing Geometric Series In Summation Notation . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
