A Magnetic Field Induced In The Conductor Carrying The Current
Muz Play
Mar 27, 2025 · 7 min read
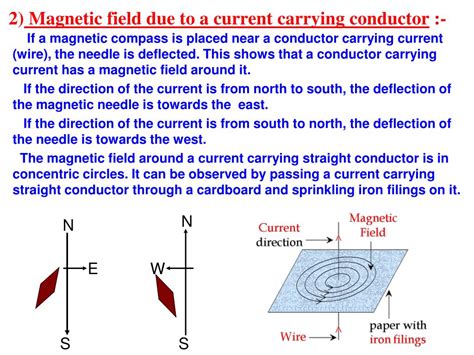
Table of Contents
A Magnetic Field Induced in a Current-Carrying Conductor: A Deep Dive
The interaction between electricity and magnetism is a cornerstone of modern physics, underpinning technologies from electric motors to MRI machines. A fundamental aspect of this interaction is the generation of a magnetic field around a conductor carrying an electric current. This phenomenon, predicted by Ampère's law and demonstrably confirmed through countless experiments, is crucial to understanding numerous electrical and electromagnetic phenomena. This article will delve into the intricacies of this magnetic field, exploring its characteristics, governing laws, applications, and implications.
Understanding the Basics: Current and Magnetic Fields
Before we delve into the specifics of the magnetic field induced in a conductor, it's essential to establish a fundamental understanding of electric current and magnetic fields.
Electric Current: The Flow of Charge
Electric current, denoted by the symbol I, represents the rate of flow of electric charge. In a metallic conductor, this charge is carried by electrons, which are negatively charged particles. When a potential difference (voltage) is applied across a conductor, an electric field is established, driving the electrons to move in a specific direction, constituting an electric current. The unit of current is the ampere (A), representing one coulomb of charge passing a point per second.
Magnetic Fields: An Invisible Force
A magnetic field, represented by the symbol B, is a vector field that exerts a force on moving charges. This force, described by the Lorentz force law, is proportional to the charge's velocity and the strength of the magnetic field. Unlike electric fields, which emanate from electric charges, magnetic fields are generated by moving charges (currents) or changing electric fields. The unit of magnetic field strength is the tesla (T).
Ampère's Law: The Foundation of Magnetic Field Generation
The relationship between an electric current and the magnetic field it generates is fundamentally described by Ampère's law. In its integral form, Ampère's law states:
∮ B ⋅ dl = μ₀I
Where:
- B is the magnetic field vector
- dl is an infinitesimal element of the closed loop path around the conductor
- μ₀ is the permeability of free space (a constant)
- I is the current enclosed by the loop
This equation tells us that the line integral of the magnetic field around a closed loop is proportional to the current passing through the loop. This implies that a current creates a magnetic field that circulates around it. The direction of the magnetic field is determined by the right-hand rule: if you curl the fingers of your right hand in the direction of the current, your thumb points in the direction of the magnetic field.
Applying Ampère's Law: The Case of a Straight Conductor
For a long, straight conductor carrying a current I, the magnetic field lines form concentric circles around the conductor. The magnitude of the magnetic field at a distance r from the conductor is given by:
B = (μ₀I) / (2πr)
This equation shows that the magnetic field strength is inversely proportional to the distance from the conductor. This means the field is strongest near the conductor and weakens as the distance increases.
Factors Affecting the Magnetic Field Strength
Several factors influence the strength of the magnetic field induced around a current-carrying conductor:
-
Magnitude of the Current (I): A larger current produces a stronger magnetic field. This is directly proportional, as shown in Ampère's law.
-
Distance from the Conductor (r): As mentioned before, the magnetic field strength is inversely proportional to the distance from the conductor. The closer you are, the stronger the field.
-
Permeability of the Medium (μ): The permeability of the surrounding medium affects the strength of the magnetic field. Ferromagnetic materials, like iron, have a much higher permeability than air or vacuum, resulting in a significantly stronger magnetic field. This principle is used in electromagnets.
-
Shape of the Conductor: The shape of the conductor significantly influences the magnetic field distribution. For example, a solenoid (a coil of wire) produces a much more concentrated and uniform magnetic field inside the coil compared to a straight wire.
Beyond Straight Wires: Magnetic Fields in More Complex Geometries
While the straight wire example provides a good starting point, real-world applications often involve conductors with more complex geometries. Understanding the magnetic field distribution in these cases requires more sophisticated techniques, often involving numerical methods or applying Ampère's law in more complex integral forms.
Solenoids and Toroids: Concentrating the Magnetic Field
Solenoids, coils of wire wound tightly together, are commonly used to generate relatively uniform magnetic fields within their core. The magnetic field inside a solenoid is approximately uniform and parallel to the axis of the solenoid. The field strength is given by:
B = μ₀nI
Where n is the number of turns per unit length of the solenoid.
Toroids, doughnut-shaped coils, also produce a confined magnetic field. Unlike the solenoid, the magnetic field is predominantly confined within the toroid itself, with minimal field leakage outside.
Complex Shapes and Numerical Methods
For conductors with highly irregular shapes, calculating the magnetic field analytically becomes exceedingly difficult, if not impossible. In these scenarios, numerical methods like finite element analysis (FEA) are employed to approximate the magnetic field distribution. These methods divide the problem into smaller, manageable elements and solve Ampère's law numerically for each element.
Applications of Magnetic Fields Induced by Current
The phenomenon of a magnetic field induced by a current is fundamental to numerous technologies and applications. Here are some notable examples:
-
Electromagnets: Electromagnets use coils of wire carrying current to create powerful magnetic fields. They are used in a wide range of applications, including electric motors, generators, magnetic resonance imaging (MRI) machines, and magnetic levitation (Maglev) trains.
-
Electric Motors and Generators: These devices rely on the interaction between magnetic fields and currents to convert electrical energy into mechanical energy (motors) or vice versa (generators). The magnetic field generated by the current in the motor's coils interacts with permanent magnets or other electromagnets, resulting in rotational motion.
-
Loudspeakers: In loudspeakers, an electric current passing through a coil placed within a magnetic field generates a force that moves the speaker cone, producing sound waves.
-
Magnetic Recording: Hard disk drives and magnetic tapes use magnetic fields to store information. Data is written by magnetizing tiny regions of a magnetic material using a current-carrying coil.
-
Particle Accelerators: In particle accelerators, strong magnetic fields, generated by large electromagnets, are used to guide and accelerate charged particles to extremely high speeds.
-
Magnetic Resonance Imaging (MRI): MRI machines use powerful magnetic fields and radio waves to produce detailed images of the inside of the human body. The magnetic field aligns the nuclear spins of atoms in the body, and radio waves are used to perturb and detect these spins, providing information about the tissue structure.
Further Considerations: Skin Effect and Proximity Effect
At high frequencies, the distribution of current within a conductor becomes non-uniform due to phenomena called the skin effect and proximity effect.
Skin Effect: Current Concentration at the Surface
The skin effect describes the tendency of alternating current (AC) to concentrate near the surface of a conductor at higher frequencies. This is due to the opposing magnetic field generated by the current itself, which pushes the current towards the outer layers of the conductor. The effective resistance of the conductor increases at high frequencies due to the reduced cross-sectional area available for current flow.
Proximity Effect: Mutual Induction Between Conductors
The proximity effect refers to the non-uniform distribution of current in multiple conductors running parallel to each other. The magnetic field generated by one conductor induces a current in the neighboring conductor, causing the current distribution to become uneven. This effect is particularly noticeable at high frequencies and can lead to increased losses in power transmission lines and electronic circuits.
Conclusion: A Fundamental Electromagnetic Phenomenon
The generation of a magnetic field around a current-carrying conductor is a fundamental principle in electromagnetism with far-reaching consequences. Ampère's law provides a mathematical framework for understanding this phenomenon, while the factors influencing magnetic field strength allow for controlled manipulation and application. From simple electromagnets to sophisticated medical imaging devices, the interplay between electricity and magnetism, rooted in this fundamental principle, continues to shape modern technology and scientific advancements. A deeper understanding of this interaction allows for innovation and improvements in countless technologies that rely on the precise control and utilization of magnetic fields.
Latest Posts
Latest Posts
-
Find Standard Matrix Of Linear Transformation
Mar 30, 2025
-
Is Delta H Products Minus Reactants
Mar 30, 2025
-
What Color Does Iodine Turn In The Presence Of Starch
Mar 30, 2025
-
How To Draw Lewis Structures For Ionic Compounds
Mar 30, 2025
-
Why Do Things Dissolve Faster In Hot Water
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about A Magnetic Field Induced In The Conductor Carrying The Current . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
