A State Function Is Best Described As
Muz Play
Apr 01, 2025 · 6 min read
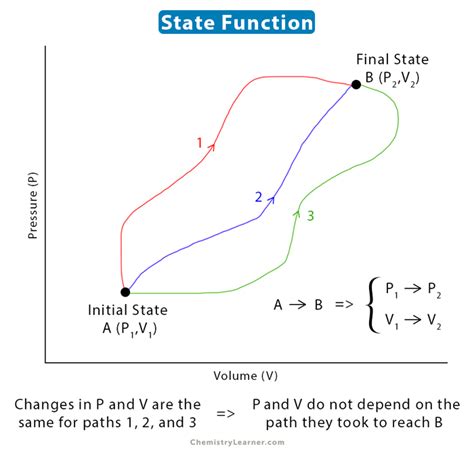
Table of Contents
A State Function: A Comprehensive Guide
A state function, in the realm of thermodynamics and other scientific disciplines, is a property whose value depends only on the current state of the system, not on the path taken to reach that state. This seemingly simple definition underpins a vast array of concepts and calculations crucial to understanding physical processes. Understanding state functions is fundamental to mastering thermodynamics, physical chemistry, and even certain aspects of engineering. This article will explore state functions in detail, explaining their properties, providing illustrative examples, and contrasting them with path functions.
Defining State Functions: The Essence of "State"
The key to understanding state functions lies in the word "state." A system's state is defined by a set of measurable properties, typically including:
- Temperature (T): A measure of the average kinetic energy of the particles in a system.
- Pressure (P): The force exerted per unit area by the system on its surroundings.
- Volume (V): The amount of space occupied by the system.
- Internal Energy (U): The total energy of the system, including kinetic and potential energies of its constituent particles.
- Enthalpy (H): A measure of the total heat content of a system at constant pressure.
- Entropy (S): A measure of the randomness or disorder within a system.
- Gibbs Free Energy (G): A thermodynamic potential that indicates the maximum reversible work that may be performed by a thermodynamic system at a constant temperature and pressure.
If you know the values of these properties (or a sufficient subset thereof, depending on the system), you have completely specified the system's state. Importantly, the path by which the system reached this state is irrelevant. This is the defining characteristic of a state function.
The Path Independence Principle
The path independence principle is the cornerstone of state functions. Imagine two different pathways leading to the same final state of a system. For a state function, the change in the function's value between the initial and final states will be identical regardless of the chosen pathway. This is in stark contrast to path functions, discussed later.
Illustrative Example: Consider climbing a mountain. Your altitude is a state function. Whether you take a steep, challenging route or a gentler, longer route, your change in altitude between the base and the summit will be the same. The path taken only affects the effort expended, not the final altitude.
Key Properties of State Functions
Several key properties distinguish state functions from other thermodynamic quantities:
- Path Independence: As highlighted above, the change in a state function depends solely on the initial and final states, not the path connecting them.
- Exact Differentials: State functions are described using exact differentials. In calculus, an exact differential is a differential form that can be expressed as the total differential of a function. This means there exists a function whose derivative is the differential form.
- Additivity: The value of a state function for a combined system is the sum of the values for each individual subsystem.
- Cyclic Integrals: The integral of a state function around a closed loop (returning to the initial state) is always zero. This reflects the path independence property; if the system returns to its initial state, the overall change in the state function is zero.
Examples of State Functions
Many crucial properties in thermodynamics and physical chemistry are state functions. Here are some of the most important:
- Internal Energy (U): Represents the total energy contained within a system. The change in internal energy (ΔU) depends only on the initial and final states of the system.
- Enthalpy (H): Often used in constant-pressure processes, enthalpy is defined as H = U + PV. Like internal energy, the change in enthalpy (ΔH) is path-independent.
- Entropy (S): A measure of the disorder or randomness of a system. The change in entropy (ΔS) is a state function, reflecting the overall change in disorder irrespective of the process's details.
- Gibbs Free Energy (G): A thermodynamic potential that predicts the spontaneity of a process at constant temperature and pressure. The change in Gibbs free energy (ΔG) is a state function.
- Helmholtz Free Energy (A): Similar to Gibbs free energy, but used for constant volume processes. The change in Helmholtz free energy (ΔA) is also a state function.
- Volume (V): The volume occupied by a system is a state function. The change in volume (ΔV) depends only on the initial and final volumes, regardless of how the volume changed.
- Temperature (T) and Pressure (P): Both temperature and pressure are state functions. Their values depend solely on the current state of the system and not on its history.
Path Functions: A Contrast with State Functions
To fully appreciate state functions, it's crucial to understand path functions. Path functions are properties whose values do depend on the path taken to reach a particular state. The change in a path function is not simply a function of the initial and final states.
Examples of Path Functions
- Heat (q): The amount of heat transferred to or from a system depends significantly on the pathway taken. The same initial and final states can have vastly different heat transfers depending on the process.
- Work (w): Similar to heat, the amount of work done on or by a system depends heavily on the path. Different processes between the same initial and final states may involve drastically different amounts of work.
Key Differences between State and Path Functions
| Feature | State Function | Path Function |
|---|---|---|
| Path Dependence | Independent | Dependent |
| Exact Differential | Yes | No |
| Cyclic Integral | Always zero | Non-zero, depends on the path |
| Representation | ΔF = F(final) - F(initial) | No simple equation relating initial and final states |
Applications of State Functions
State functions are indispensable tools in various scientific and engineering disciplines. Their path independence allows for significant simplifications in calculations.
Thermodynamics
State functions are at the heart of thermodynamics. They are essential for:
- Calculating changes in internal energy, enthalpy, and entropy. These calculations are crucial for predicting the spontaneity and equilibrium of chemical and physical processes.
- Determining the maximum work achievable by a system. This is particularly relevant in engineering applications involving engines and power generation.
- Analyzing phase transitions and chemical reactions. State functions help determine the equilibrium conditions and predict the direction of change.
Physical Chemistry
State functions are critical in physical chemistry for:
- Understanding chemical equilibrium. State functions are used to calculate equilibrium constants and predict the position of equilibrium.
- Determining the spontaneity of reactions. The Gibbs free energy change (ΔG) is a key indicator of reaction spontaneity.
- Analyzing electrochemical processes. State functions are essential in understanding cell potentials and electrochemical reactions.
Engineering
State functions are applied in various engineering contexts:
- Designing efficient engines and power generation systems. Understanding the changes in state functions helps maximize work output and minimize energy loss.
- Developing chemical processes. State functions provide crucial insights for optimizing reaction conditions and yields.
- Analyzing material properties. State functions contribute to understanding the thermodynamic behavior of materials under various conditions.
Conclusion: The Power of State Functions
State functions represent a powerful concept in thermodynamics and related fields. Their path independence simplifies complex calculations and provides a robust framework for understanding physical and chemical processes. Understanding the nature of state functions is vital for anyone studying thermodynamics, physical chemistry, or related disciplines. By grasping the core principles of state functions, one gains a deeper understanding of the fundamental laws governing energy, entropy, and the behavior of matter. This comprehension facilitates problem-solving, analysis, and the design of more efficient and sustainable systems. The continued application and exploration of state functions remain crucial for scientific advancement and technological innovation.
Latest Posts
Latest Posts
-
Activation Energy For The Forward Reaction
Apr 02, 2025
-
Base Excision Repair Vs Mismatch Repair
Apr 02, 2025
-
Is Argon Metal Nonmetal Or Metalloid
Apr 02, 2025
-
What Is A Limiting Amino Acid In A Protein
Apr 02, 2025
-
Under What Conditions Are Gases Most Likely To Behave Ideally
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about A State Function Is Best Described As . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
