Addition Subtraction Multiplication And Division Of Polynomials
Muz Play
Apr 05, 2025 · 5 min read
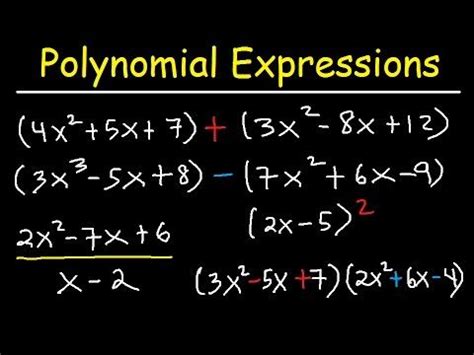
Table of Contents
Addition, Subtraction, Multiplication, and Division of Polynomials: A Comprehensive Guide
Polynomials are fundamental algebraic expressions that form the bedrock of many advanced mathematical concepts. Understanding how to perform the four basic arithmetic operations – addition, subtraction, multiplication, and division – on polynomials is crucial for success in algebra and beyond. This comprehensive guide will delve into each operation, providing clear explanations, examples, and strategies to master these essential skills.
Understanding Polynomials
Before diving into the operations, let's refresh our understanding of polynomials. A polynomial is an expression consisting of variables (often denoted by x), coefficients, and exponents, combined using addition, subtraction, and multiplication. Terms are separated by addition or subtraction. Each term is a product of a coefficient and a variable raised to a non-negative integer power. For example:
- 3x² + 5x - 7: This is a polynomial with three terms.
- x⁴ - 2x³ + x: This is a polynomial with three terms.
- 5: This is a polynomial (a constant polynomial).
- x²y + 2xy² - 3: This is a polynomial in two variables.
The degree of a polynomial is the highest power of the variable in the expression. For instance, the degree of 3x² + 5x - 7 is 2, while the degree of x⁴ - 2x³ + x is 4.
Addition of Polynomials
Adding polynomials is a straightforward process. It involves combining like terms, meaning terms with the same variable raised to the same power. We simply add the coefficients of like terms.
Example:
Add (3x² + 5x - 7) and (x² - 2x + 4).
- Identify like terms: 3x² and x² are like terms; 5x and -2x are like terms; -7 and 4 are like terms.
- Combine like terms: (3x² + x²) + (5x - 2x) + (-7 + 4)
- Simplify: 4x² + 3x - 3
Therefore, (3x² + 5x - 7) + (x² - 2x + 4) = 4x² + 3x - 3
Subtraction of Polynomials
Subtraction of polynomials is similar to addition, but with a crucial difference: we subtract the coefficients of like terms. Remember that subtracting a polynomial is equivalent to adding its negative.
Example:
Subtract (2x³ - 4x + 6) from (5x³ + 2x² - x + 1).
- Rewrite as addition: (5x³ + 2x² - x + 1) + (-2x³ + 4x - 6) Notice how we changed the signs of each term in the polynomial being subtracted.
- Combine like terms: (5x³ - 2x³) + 2x² + (-x + 4x) + (1 - 6)
- Simplify: 3x³ + 2x² + 3x - 5
Therefore, (5x³ + 2x² - x + 1) - (2x³ - 4x + 6) = 3x³ + 2x² + 3x - 5
Multiplication of Polynomials
Multiplying polynomials involves applying the distributive property (often called the FOIL method for binomials). Each term in the first polynomial must be multiplied by each term in the second polynomial. Then, combine like terms to simplify the result.
Example 1: Multiplying a monomial by a polynomial
Multiply 2x by (3x² - 4x + 5).
- Distribute: 2x * 3x² - 2x * 4x + 2x * 5
- Simplify: 6x³ - 8x² + 10x
Therefore, 2x(3x² - 4x + 5) = 6x³ - 8x² + 10x
Example 2: Multiplying two binomials (FOIL Method)
Multiply (x + 2) by (x - 3).
- FOIL: First (xx), Outer (x-3), Inner (2x), Last (2-3)
- Expand: x² - 3x + 2x - 6
- Simplify: x² - x - 6
Therefore, (x + 2)(x - 3) = x² - x - 6
Example 3: Multiplying two polynomials of higher degree
Multiply (2x² + x - 1) by (x² - 3x + 2).
This requires a more systematic approach than FOIL. Multiply each term in the first polynomial by each term in the second, then combine like terms.
- Expand: 2x²(x² - 3x + 2) + x(x² - 3x + 2) - 1(x² - 3x + 2)
- Distribute: 2x⁴ - 6x³ + 4x² + x³ - 3x² + 2x - x² + 3x - 2
- Combine like terms: 2x⁴ + (-6x³ + x³) + (4x² - 3x² - x²) + (2x + 3x) - 2
- Simplify: 2x⁴ - 5x³ + 0x² +5x - 2
Therefore, (2x² + x - 1)(x² - 3x + 2) = 2x⁴ - 5x³ + 5x - 2
Division of Polynomials
Polynomial division is more complex than the other operations. There are two main methods: long division and synthetic division. Long division is more general and works for all polynomial divisions, while synthetic division is a shortcut that only works when dividing by a linear binomial (x - c).
Long Division of Polynomials
Long division of polynomials is analogous to long division of numbers.
Example:
Divide (3x³ + 2x² - 5x + 4) by (x + 2).
- Set up the long division:
x + 2 | 3x³ + 2x² - 5x + 4 - Divide the leading term of the dividend (3x³) by the leading term of the divisor (x): 3x²
- Multiply the quotient (3x²) by the divisor (x + 2): 3x³ + 6x²
- Subtract this result from the dividend: (3x³ + 2x² - 5x + 4) - (3x³ + 6x²) = -4x² - 5x + 4
- Bring down the next term (-5x): -4x² - 5x + 4
- Repeat the process: Divide -4x² by x, obtaining -4x. Multiply -4x by (x+2), obtaining -4x² - 8x. Subtract to get 3x + 4.
- Repeat again: Divide 3x by x, obtaining 3. Multiply 3 by (x+2), obtaining 3x + 6. Subtract to get -2.
- The remainder is -2.
Therefore, (3x³ + 2x² - 5x + 4) / (x + 2) = 3x² - 4x + 3 - 2/(x+2)
Synthetic Division of Polynomials
Synthetic division is a streamlined method for dividing a polynomial by a linear binomial of the form (x - c).
Example:
Divide (2x³ - 7x² + 5x + 2) by (x - 2) using synthetic division.
- Set up the synthetic division: Use 'c' (in this case, 2) and the coefficients of the dividend.
2 | 2 -7 5 2 - Bring down the first coefficient (2):
2 | 2 -7 5 2 2 - Multiply 2 by 2 (c), and add to the next coefficient (-7): 2 * 2 = 4; -7 + 4 = -3
2 | 2 -7 5 2 2 -3 - Repeat the process: 2 * -3 = -6; 5 + (-6) = -1; 2 * -1 = -2; 2 + (-2) = 0
2 | 2 -7 5 2 2 -6 -2 ---------------- 2 -3 -1 0
The last number (0) is the remainder. The other numbers are the coefficients of the quotient.
Therefore, (2x³ - 7x² + 5x + 2) / (x - 2) = 2x² - 3x - 1
Mastering these four operations on polynomials is a fundamental step in your algebraic journey. Practice is key – the more you work with these techniques, the more confident and proficient you'll become. Remember to always double-check your work and look for opportunities to simplify your answers. With consistent effort, you'll gain a deep understanding of polynomials and their manipulations.
Latest Posts
Latest Posts
-
Used To Help Substances Enter Or Exit The Cell Membrane
Apr 05, 2025
-
Verify That Is A Solution To The Differential Equation
Apr 05, 2025
-
Gaining Or Losing Electrons Is Called
Apr 05, 2025
-
How Sociology Differs From Other Social Sciences
Apr 05, 2025
-
Do Ionic Compounds Have High Boiling Points
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Addition Subtraction Multiplication And Division Of Polynomials . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
