Angular Momentum Operator In Spherical Coordinates
Muz Play
Apr 02, 2025 · 6 min read
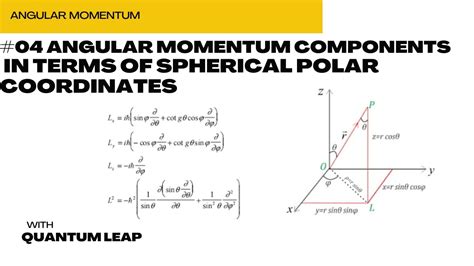
Table of Contents
Angular Momentum Operator in Spherical Coordinates: A Comprehensive Guide
The angular momentum operator is a fundamental concept in quantum mechanics, playing a crucial role in understanding the behavior of atomic and subatomic particles. While often introduced in Cartesian coordinates, its representation in spherical coordinates proves significantly more insightful, especially when dealing with systems exhibiting spherical symmetry, like atoms. This article provides a comprehensive exploration of the angular momentum operator in spherical coordinates, delving into its mathematical formulation, properties, and physical significance.
Understanding the Angular Momentum Operator
Before diving into the intricacies of spherical coordinates, let's establish a foundational understanding of the angular momentum operator itself. Angular momentum, denoted by L, represents the rotational analogue of linear momentum. Classically, it's defined as the cross product of the position vector r and the linear momentum vector p:
L = r x p
In quantum mechanics, these classical quantities become operators. The linear momentum operator p is represented as -iħ∇, where ħ is the reduced Planck constant and ∇ is the del operator. Therefore, the angular momentum operator becomes an operator acting on wavefunctions.
Cartesian Representation of the Angular Momentum Operator
In Cartesian coordinates, the angular momentum operator is expressed as three components:
- L<sub>x</sub> = y p<sub>z</sub> - z p<sub>y</sub> = -iħ(y ∂/∂z - z ∂/∂y)
- L<sub>y</sub> = z p<sub>x</sub> - x p<sub>z</sub> = -iħ(z ∂/∂x - x ∂/∂z)
- L<sub>z</sub> = x p<sub>y</sub> - y p<sub>x</sub> = -iħ(x ∂/∂y - y ∂/∂x)
The square of the total angular momentum operator, L², is given by:
L² = L<sub>x</sub>² + L<sub>y</sub>² + L<sub>z</sub>²
These operators satisfy specific commutation relations, which are fundamental to understanding the quantization of angular momentum:
- [L<sub>x</sub>, L<sub>y</sub>] = iħL<sub>z</sub>
- [L<sub>y</sub>, L<sub>z</sub>] = iħL<sub>x</sub>
- [L<sub>z</sub>, L<sub>x</sub>] = iħL<sub>y</sub>
- [L², L<sub>x</sub>] = [L², L<sub>y</sub>] = [L², L<sub>z</sub>] = 0
These commutation relations imply that only one component of the angular momentum can be measured simultaneously with the total angular momentum. Conventionally, L<sub>z</sub> is chosen for this simultaneous measurement.
Transformation to Spherical Coordinates
The true power of the angular momentum operator becomes apparent when expressed in spherical coordinates. The transformation from Cartesian (x, y, z) to spherical coordinates (r, θ, φ) is given by:
- x = r sin θ cos φ
- y = r sin θ sin φ
- z = r cos θ
The del operator (∇) in spherical coordinates is:
∇ = (∂/∂r)ê<sub>r</sub> + (1/r)(∂/∂θ)ê<sub>θ</sub> + (1/(r sin θ))(∂/∂φ)ê<sub>φ</sub>
where ê<sub>r</sub>, ê<sub>θ</sub>, and ê<sub>φ</sub> are the unit vectors in the radial, polar, and azimuthal directions, respectively. This transformation is crucial for expressing the angular momentum operator in spherical coordinates.
Spherical Coordinate Representation of the Angular Momentum Operator
Applying the coordinate transformation and the del operator in spherical coordinates to the Cartesian expressions for L<sub>x</sub>, L<sub>y</sub>, and L<sub>z</sub>, we obtain a more elegant and insightful representation. After considerable algebraic manipulation (detailed derivations can be found in advanced quantum mechanics textbooks), we arrive at:
- L<sub>z</sub> = -iħ(∂/∂φ)
This is remarkably simple: L<sub>z</sub> is purely a derivative with respect to the azimuthal angle φ. This directly reflects the fact that L<sub>z</sub> represents the projection of angular momentum onto the z-axis, which is directly related to the rotation around the z-axis.
The expressions for L<sub>x</sub> and L<sub>y</sub> are more complex:
- L<sub>x</sub> = iħ(sin φ ∂/∂θ + cot θ cos φ ∂/∂φ)
- L<sub>y</sub> = -iħ(cos φ ∂/∂θ - cot θ sin φ ∂/∂φ)
While less intuitive at first glance, these expressions, combined with L<sub>z</sub>, allow for the complete description of the angular momentum operator in spherical coordinates.
The Total Angular Momentum Operator (L²) in Spherical Coordinates
The expression for the total angular momentum operator L² in spherical coordinates simplifies significantly:
L² = -ħ²(1/sin θ)(∂/∂θ)(sin θ ∂/∂θ) + (-ħ²/sin²θ)(∂²/∂φ²)
This expression is crucial because it's independent of the radial coordinate 'r'. This independence is a direct consequence of the rotational symmetry inherent in many physical systems. This allows us to separate the radial part of the wavefunction from the angular part when solving the Schrödinger equation for such systems.
Eigenfunctions and Eigenvalues of L² and L<sub>z</sub>
The eigenfunctions of L² and L<sub>z</sub> are the spherical harmonics, denoted as Y<sub>lm</sub>(θ, φ), where 'l' is the angular momentum quantum number (l = 0, 1, 2, ...) and 'm' is the magnetic quantum number (m = -l, -l+1, ..., 0, ..., l-1, l).
- L² Y<sub>lm</sub>(θ, φ) = ħ²l(l+1) Y<sub>lm</sub>(θ, φ)
- L<sub>z</sub> Y<sub>lm</sub>(θ, φ) = ħm Y<sub>lm</sub>(θ, φ)
The spherical harmonics form a complete orthonormal set of functions on the unit sphere, crucial for expanding any angular-dependent function. Their specific forms are well-documented in mathematical physics literature and are readily available in computational packages. The quantization of angular momentum is directly evident in the eigenvalues ħ²l(l+1) and ħm.
Applications and Physical Significance
The angular momentum operator in spherical coordinates is essential in various areas of physics and chemistry:
- Atomic Physics: Understanding the structure of atoms, electron orbitals, and spectral lines relies heavily on the angular momentum operator. The quantum numbers l and m directly relate to the shape and orientation of atomic orbitals.
- Molecular Physics: Molecular rotation and vibrations are described using the angular momentum operator. The rotational energy levels of molecules are directly related to the eigenvalues of L².
- Nuclear Physics: Nuclear angular momentum plays a vital role in understanding nuclear structure and decay processes.
- Particle Physics: The intrinsic angular momentum (spin) of elementary particles is mathematically analogous to orbital angular momentum, though fundamentally distinct in its origin.
Solving the Schrödinger Equation with Spherical Coordinates
The spherical coordinate representation of the angular momentum operator simplifies the solution of the time-independent Schrödinger equation for systems with spherical symmetry. The equation often separates into radial and angular parts. The angular part is solved using the spherical harmonics, yielding the quantized angular momentum eigenvalues. The radial part then involves solving a differential equation specific to the potential.
Conclusion
The angular momentum operator in spherical coordinates provides a powerful framework for understanding the rotational properties of quantum systems. Its elegant mathematical form, coupled with the use of spherical harmonics, allows for efficient analysis and solutions to numerous problems in atomic, molecular, nuclear, and particle physics. The quantization of angular momentum, directly revealed through its eigenvalues, is a cornerstone of quantum mechanics and a testament to the power of this operator. Further exploration of this topic necessitates delving into the mathematical details of the transformation, the solution of the angular part of the Schrödinger equation, and the properties of the spherical harmonics. However, this article has laid a solid foundation for a deeper understanding of this crucial quantum mechanical concept.
Latest Posts
Latest Posts
-
What Accounts Appear On A Post Closing Trial Balance
Apr 03, 2025
-
Gross Anatomy Of Cow Eye Labeled
Apr 03, 2025
-
What Are The 12 Elements Of Culture
Apr 03, 2025
-
What Is The Domain Of X
Apr 03, 2025
-
Examples Of Straw Man Fallacy In Advertising
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Angular Momentum Operator In Spherical Coordinates . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
