Area Of A Parallelogram Cross Product
Muz Play
Apr 01, 2025 · 6 min read
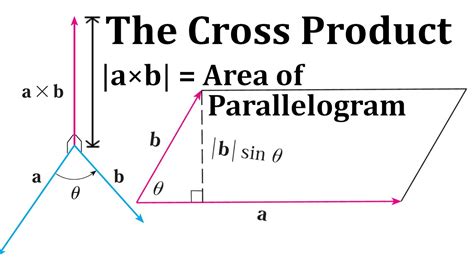
Table of Contents
Area of a Parallelogram: A Deep Dive into the Cross Product
The area of a parallelogram is a fundamental concept in geometry, finding applications in various fields like physics, engineering, and computer graphics. While traditional methods exist to calculate this area, using the cross product offers an elegant and powerful approach, especially when dealing with vectors in three-dimensional space. This article will delve into the intricacies of calculating the area of a parallelogram using the cross product, exploring its theoretical underpinnings, practical applications, and related concepts.
Understanding the Parallelogram and its Area
A parallelogram is a quadrilateral with opposite sides parallel and equal in length. Its area is intuitively understood as the product of its base and its corresponding height. However, this simple formula becomes less straightforward when dealing with parallelograms positioned arbitrarily in space. This is where the power of vector mathematics and the cross product come into play.
Defining the Parallelogram using Vectors
To utilize the cross product effectively, we need to represent the parallelogram's sides using vectors. Let's consider two vectors, a and b, which represent two adjacent sides of the parallelogram. These vectors define the parallelogram completely, regardless of its orientation in space. The length of vector a represents the length of one side of the parallelogram, and the length of vector b represents the length of the adjacent side.
The area of the parallelogram formed by these two vectors is directly related to the magnitude of their cross product.
Introducing the Cross Product
The cross product, also known as the vector product, is a binary operation on two vectors in three-dimensional space. The result of the cross product is another vector that is orthogonal (perpendicular) to both of the original vectors. This orthogonality is crucial in understanding its connection to the area of a parallelogram.
The Cross Product Formula
The cross product of two vectors a = (a₁, a₂, a₃) and b = (b₁, b₂, b₃) is calculated as follows:
a x b = (a₂b₃ - a₃b₂, a₃b₁ - a₁b₃, a₁b₂ - a₂b₁)
This formula might seem daunting at first, but it's a systematic process of calculating the components of the resulting vector. Notice the cyclical pattern in the subscripts, which aids memorization.
Geometric Interpretation of the Cross Product
The magnitude (length) of the cross product vector |a x b| is directly related to the area of the parallelogram formed by vectors a and b. Specifically:
Area of Parallelogram = |a x b|
This equation elegantly connects the algebraic calculation of the cross product to the geometric property of area. The magnitude of the cross product represents the area of the parallelogram because it captures the effect of both the lengths of the sides and the angle between them.
The Angle Between the Vectors
The magnitude of the cross product is also related to the angle θ between the two vectors a and b. This relationship is given by:
|a x b| = |a| |b| sin(θ)
This formula highlights that the area of the parallelogram is maximized when the angle between the vectors is 90 degrees (sin(90°) = 1). When the vectors are parallel (θ = 0° or 180°), the area becomes zero, as sin(0°) = sin(180°) = 0.
Calculating the Area: Step-by-Step Examples
Let's illustrate the calculation of the parallelogram's area using the cross product with several examples.
Example 1: Simple Vectors
Consider vectors a = (1, 2, 3) and b = (4, 5, 6).
-
Calculate the cross product:
a x b = (26 - 35, 34 - 16, 15 - 24) = (-3, 6, -3)
-
Find the magnitude of the cross product:
|a x b| = √((-3)² + 6² + (-3)²) = √(9 + 36 + 9) = √54
-
The area of the parallelogram is √54 square units.
Example 2: Vectors with Zero Components
Let's analyze vectors where one or more components are zero. Consider a = (2, 0, 0) and b = (0, 3, 0).
-
Calculate the cross product:
a x b = (00 - 03, 00 - 20, 23 - 00) = (0, 0, 6)
-
Find the magnitude:
|a x b| = √(0² + 0² + 6²) = 6
-
The area is 6 square units. This example demonstrates how the cross product simplifies when dealing with vectors aligned with coordinate axes.
Example 3: Vectors in a Plane
Even if the vectors themselves lie in a plane (like the xy-plane), the cross product still correctly determines the area. Consider a = (1, 2, 0) and b = (3, 1, 0).
-
Calculate the cross product:
a x b = (20 - 01, 03 - 10, 11 - 23) = (0, 0, -5)
-
Find the magnitude:
|a x b| = √(0² + 0² + (-5)²) = 5
-
The area is 5 square units. This confirms the versatility of the cross product regardless of the vector's orientation in 3D space.
Applications of the Cross Product and Parallelogram Area
The ability to calculate the area of a parallelogram using the cross product has numerous applications in various fields:
Physics:
-
Torque: The torque on a rigid body is calculated as the cross product of the lever arm vector and the force vector. The magnitude of the torque is directly related to the area of the parallelogram formed by these vectors.
-
Angular Momentum: Similar to torque, angular momentum involves the cross product of a position vector and a momentum vector. The area of the parallelogram defined by these vectors is relevant in understanding the angular momentum's magnitude.
-
Magnetic Force: The force exerted on a charged particle moving in a magnetic field is determined using the cross product of the velocity and magnetic field vectors. The area of the parallelogram helps in understanding the force's magnitude.
Computer Graphics:
-
Surface Normals: In 3D computer graphics, surface normals (vectors perpendicular to a surface) are often calculated using the cross product. The parallelogram area isn't directly used here, but the cross product's ability to generate orthogonal vectors is fundamental.
-
Polygon Area Calculation: The cross product provides an efficient way to calculate the area of polygons in 3D space by breaking down the polygon into triangles and applying the cross product to each triangle.
Engineering:
-
Mechanical Engineering: The cross product is extensively used in calculating moments and torques in various mechanical systems, leveraging the parallelogram area concept.
-
Civil Engineering: Structural analysis frequently uses vector calculations, including cross products, to determine forces and moments acting on structures.
Beyond the Parallelogram: Applications to Triangles
The cross product's usefulness extends beyond parallelograms. Since a triangle is half of a parallelogram, its area can also be efficiently calculated using the cross product:
Area of Triangle = (1/2) |a x b|
Where a and b are vectors representing two sides of the triangle.
This formula provides a concise and computationally efficient method for calculating the area of a triangle in 3D space.
Conclusion
The cross product provides a powerful and elegant method for calculating the area of a parallelogram, offering a significant advantage over traditional geometric approaches, particularly in three-dimensional space. Its applicability extends to various fields, highlighting its importance as a fundamental concept in mathematics and its numerous practical applications in science, engineering, and computer graphics. Understanding the cross product and its geometric interpretation enhances one's ability to solve complex problems in these disciplines. The ability to move between the algebraic representation of the cross product and its geometric meaning is a key skill for mastering this valuable tool.
Latest Posts
Latest Posts
-
Find The Equation Of The Vertical Line
Apr 02, 2025
-
Electron Configuration For Copper And Chromium
Apr 02, 2025
-
Confidence Interval Calculator With Two Samples
Apr 02, 2025
-
Lewis Base Vs Bronsted Lowry Base
Apr 02, 2025
-
What Is Max Webers Definition Of Social Status Based On
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Area Of A Parallelogram Cross Product . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
