Colligative Properties Freezing Point Depression Lab
Muz Play
Apr 02, 2025 · 7 min read
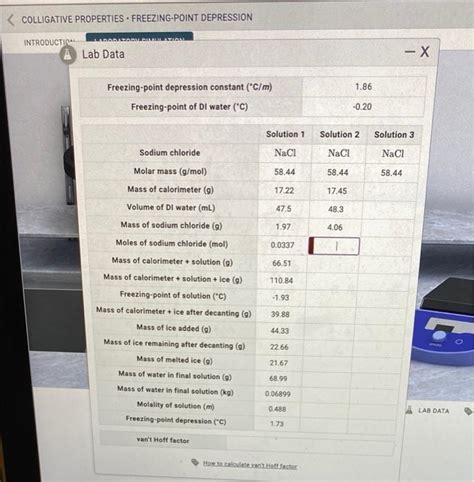
Table of Contents
Colligative Properties: A Deep Dive into Freezing Point Depression Lab Experiments
Understanding colligative properties is fundamental in chemistry. These properties depend solely on the concentration of solute particles in a solution, not their identity. Freezing point depression is a prime example, where the freezing point of a solvent is lowered when a solute is added. This lab explores this phenomenon in detail, examining the theoretical principles, experimental procedure, data analysis, and potential sources of error.
What are Colligative Properties?
Colligative properties are macroscopic properties of a solution that depend only on the number of solute particles present, not on the type of solute particles. Four main colligative properties are:
- Freezing point depression: The decrease in the freezing point of a solvent upon the addition of a solute.
- Boiling point elevation: The increase in the boiling point of a solvent upon the addition of a solute.
- Vapor pressure lowering: The decrease in the vapor pressure of a solvent upon the addition of a solute (Raoult's Law).
- Osmotic pressure: The pressure required to prevent the flow of solvent across a semipermeable membrane from a region of low solute concentration to a region of high solute concentration.
These properties arise because the solute particles disrupt the intermolecular forces within the solvent, making it more difficult for the solvent molecules to transition between phases (solid to liquid, liquid to gas).
Freezing Point Depression: The Focus of Our Experiment
Freezing point depression is directly proportional to the molality (moles of solute per kilogram of solvent) of the solution. This relationship is described by the equation:
ΔT<sub>f</sub> = K<sub>f</sub> * m * i
Where:
- ΔT<sub>f</sub> is the freezing point depression (the difference between the freezing point of the pure solvent and the freezing point of the solution).
- K<sub>f</sub> is the cryoscopic constant (a property specific to the solvent). For water, K<sub>f</sub> = 1.86 °C/m.
- m is the molality of the solution (moles of solute per kilogram of solvent).
- i is the van't Hoff factor, representing the number of particles a solute dissociates into in solution. For non-electrolytes (e.g., sucrose), i = 1. For strong electrolytes (e.g., NaCl), i = 2 (since NaCl dissociates into Na⁺ and Cl⁻ ions). For weak electrolytes, i is between 1 and the theoretical number of ions, depending on the degree of dissociation.
Designing the Freezing Point Depression Lab Experiment
This experiment aims to verify the relationship between molality and freezing point depression. We'll use water as the solvent and different solutes to observe the effect on the freezing point.
Materials:
- Various solutes (e.g., NaCl, sucrose, urea). Choose solutes with known molar masses and different van't Hoff factors.
- Distilled water
- Beakers
- Graduated cylinders
- Thermometers (accurate to at least 0.1 °C)
- Stirrers
- Ice bath
- Balance (accurate to at least 0.01 g)
Procedure:
-
Prepare solutions: Accurately weigh out a specific mass of each solute and dissolve it in a known mass of distilled water to create solutions of different molalities. Ensure you calculate the molality precisely. Multiple solutions of varying concentrations of the same solute should be prepared.
-
Measure the freezing point of pure water: Place a beaker containing distilled water into an ice bath. Stir gently and monitor the temperature until it reaches and remains stable at 0°C. Record this temperature as the freezing point of pure water. Repeat this several times to ensure accurate readings and to establish an average value. This establishes your baseline.
-
Measure the freezing point of each solution: Repeat step 2 for each solution prepared in step 1. Carefully record the temperature as the solution freezes. Again, repeat several times to get an accurate average freezing point for each concentration. Pay attention to the rate of cooling and ensure consistent stirring to promote uniform temperature distribution within the solution.
-
Data Analysis: Calculate the freezing point depression (ΔT<sub>f</sub>) for each solution by subtracting the freezing point of the solution from the freezing point of pure water. Plot ΔT<sub>f</sub> against the molality (m) of the solution. A linear relationship should be observed, validating the equation ΔT<sub>f</sub> = K<sub>f</sub> * m * i. Determine the slope of the resulting graph. This slope should be approximately equal to K<sub>f</sub> * i. By comparing the experimental slope with the theoretical value (using the known K<sub>f</sub> for water and the theoretical van't Hoff factor for each solute), you can assess the accuracy of your experiment.
Data Analysis and Interpretation
The primary goal of the data analysis is to determine the experimental van't Hoff factor (i) for each solute. This will involve the following steps:
-
Calculate the molality (m): Convert the mass of solute to moles using its molar mass and the mass of water to kilograms.
-
Calculate the freezing point depression (ΔT<sub>f</sub>): Subtract the freezing point of the solution from the freezing point of pure water.
-
Calculate the experimental van't Hoff factor (i): Rearrange the freezing point depression equation to solve for i: i = ΔT<sub>f</sub> / (K<sub>f</sub> * m).
-
Compare experimental and theoretical i: Compare the experimental i values with the theoretical i values for each solute. Discrepancies may arise from experimental errors or deviations from ideal behavior.
-
Graphical Analysis: Plot ΔT<sub>f</sub> versus molality (m). The slope of the best-fit line should approximate K<sub>f</sub>*i. The intercept should be close to zero, indicating a true linear relationship. Analyzing the graph provides a visual representation of the relationship between freezing point depression and molality.
Potential Sources of Error and Mitigation Strategies
Several factors can contribute to error in the freezing point depression experiment. These include:
-
Inaccurate measurements: Precise measurements of solute mass, water mass, and temperature are crucial. Use calibrated instruments and follow proper weighing and temperature measurement techniques.
-
Impurities in the water: The presence of impurities in the water will affect the freezing point. Use distilled water to minimize this effect.
-
Supercooling: The solution might supercool (cool below its freezing point without solidifying). Gently stirring and using a seed crystal (a small ice crystal) can help to mitigate supercooling.
-
Heat transfer: Heat transfer from the surroundings can affect the temperature readings. Insulate the apparatus and conduct the experiment in a controlled environment to minimize heat transfer.
-
Non-ideal behavior: At high concentrations, intermolecular interactions between solute particles may deviate from ideality, affecting the accuracy of the van't Hoff factor. Using dilute solutions can minimize this effect.
-
Incomplete dissolution: Ensure the solute is completely dissolved before measuring the freezing point. Incomplete dissolution leads to inaccurate molality values.
-
Thermometer lag: The thermometer may not instantly reflect the actual temperature of the solution. Allow sufficient time for the thermometer to reach equilibrium before taking a reading.
Advanced Considerations and Extensions
This experiment can be expanded upon in several ways:
-
Investigating different solvents: Repeat the experiment using different solvents to explore how their cryoscopic constants affect the freezing point depression.
-
Exploring different types of solutes: Compare the freezing point depression of electrolytes and non-electrolytes at the same molality. This helps visualize the effect of the van't Hoff factor.
-
Determining molar mass: If the molar mass of the solute is unknown, the freezing point depression can be used to determine it.
Conclusion
The freezing point depression experiment offers a valuable hands-on opportunity to understand colligative properties and their applications. By carefully controlling experimental conditions and analyzing data thoroughly, students can gain a deeper appreciation for the relationship between solute concentration and the freezing point of a solution. The experiment also highlights the importance of accurate measurements and the careful consideration of potential error sources in scientific investigations. The data analysis, including the graphical representation, is essential in reinforcing the principles and drawing meaningful conclusions from the experimental findings. By addressing the potential sources of error and exploring advanced applications, students can further enhance their understanding of colligative properties and their significance in various scientific fields.
Latest Posts
Latest Posts
-
Why Is Immersion Oil Used With The 100x Objective
Apr 03, 2025
-
What Is Shared In A Covalent Bond
Apr 03, 2025
-
Chemical Reactions And Equations Report Sheet
Apr 03, 2025
-
Cis 1 3 Dimethylcyclohexane Chair Conformation
Apr 03, 2025
-
What Does The Bacterial Chromosome Do
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Colligative Properties Freezing Point Depression Lab . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
