Confidence Interval Calculator For 2 Proportions
Muz Play
Apr 02, 2025 · 6 min read
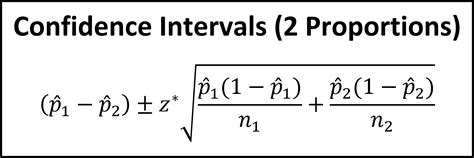
Table of Contents
Confidence Interval Calculator for 2 Proportions: A Comprehensive Guide
Understanding the difference between two proportions is crucial in various fields, from A/B testing in marketing to clinical trials in medicine. A confidence interval calculator for two proportions provides a powerful statistical tool to quantify this difference and assess its significance. This comprehensive guide will delve into the intricacies of such calculators, explaining their functionality, underlying principles, and practical applications. We'll explore different methods, address potential challenges, and offer best practices for accurate interpretation and reporting.
Understanding Confidence Intervals and Proportions
Before diving into the specifics of a two-proportion confidence interval calculator, let's establish a clear understanding of the fundamental concepts:
What is a Confidence Interval?
A confidence interval (CI) provides a range of values within which a population parameter (in this case, the difference between two proportions) is likely to lie with a certain level of confidence. This "confidence level" is typically expressed as a percentage (e.g., 95%, 99%). A 95% confidence interval means that if we were to repeat the sampling process many times, 95% of the calculated intervals would contain the true population parameter. It does not mean there's a 95% chance the true value lies within a single calculated interval.
What are Proportions?
In statistics, a proportion represents the fraction of a population that possesses a specific characteristic. For example, the proportion of website visitors who clicked on a particular advertisement, or the proportion of patients who recovered after a treatment. We often represent proportions as percentages or decimals between 0 and 1.
The Two-Proportion Z-Interval: The Core Calculation
The most common method for calculating a confidence interval for the difference between two proportions uses the normal approximation, also known as the two-proportion z-interval. This method relies on the central limit theorem, which states that the sampling distribution of the difference between two sample proportions will approximate a normal distribution under certain conditions (largely satisfied with sufficiently large sample sizes).
The formula for the confidence interval is:
(p̂₁ - p̂₂) ± Z * √[(p̂₁(1 - p̂₁)/n₁) + (p̂₂(1 - p̂₂)/n₂)]
Where:
- p̂₁ and p̂₂ are the sample proportions of the two groups.
- n₁ and n₂ are the sample sizes of the two groups.
- Z is the Z-score corresponding to the desired confidence level (e.g., 1.96 for a 95% confidence interval, 2.58 for a 99% confidence interval).
Conditions for Using the Z-Interval:
The accuracy of the z-interval relies on several assumptions:
- Independent Samples: The two samples must be independent of each other. Observations in one group should not influence the observations in the other group.
- Random Sampling: The samples should be randomly selected from their respective populations to ensure representativeness.
- Sufficient Sample Size: The sample sizes should be large enough to satisfy the following conditions for both groups: n₁p̂₁ ≥ 10, n₁(1 - p̂₁) ≥ 10, n₂p̂₂ ≥ 10, and n₂(1 - p̂₂) ≥ 10. If these conditions aren't met, consider using alternative methods like the Wilson score interval or exact methods.
Using a Confidence Interval Calculator for Two Proportions
A confidence interval calculator for two proportions simplifies this complex calculation. You typically input the following data:
- Sample Proportion 1 (p̂₁): The proportion of successes in the first group.
- Sample Size 1 (n₁): The total number of observations in the first group.
- Sample Proportion 2 (p̂₂): The proportion of successes in the second group.
- Sample Size 2 (n₂): The total number of observations in the second group.
- Confidence Level: The desired confidence level (e.g., 95%, 99%).
The calculator will then compute the confidence interval, providing the lower and upper bounds of the interval for the difference between the two proportions (p̂₁ - p̂₂).
Interpreting the Results
The output of a two-proportion confidence interval calculator is a range of values. For example, a 95% confidence interval of (0.05, 0.15) for the difference between two proportions suggests that we are 95% confident that the true difference between the two population proportions lies between 0.05 and 0.15.
Key Interpretations:
- If the interval contains 0: This indicates that there is no statistically significant difference between the two proportions at the chosen confidence level. The observed difference could be due to random chance.
- If the interval does not contain 0: This suggests a statistically significant difference between the two proportions. The direction of the difference (positive or negative) indicates which proportion is larger.
Choosing the Right Calculator and Method
While the z-interval is widely used, other methods exist, particularly for smaller sample sizes:
- Wilson Score Interval: This method is considered more accurate than the z-interval, especially when sample sizes are small or proportions are close to 0 or 1. It provides a more reliable confidence interval, particularly when dealing with small sample sizes.
- Exact Methods (e.g., Clopper-Pearson): These methods use the binomial distribution directly and are suitable for very small sample sizes. They are computationally more intensive but avoid the approximations made by the z-interval or Wilson score interval.
A good confidence interval calculator will offer options for different methods, allowing you to select the most appropriate one based on your sample size and data characteristics.
Potential Challenges and Considerations
- Multiple Comparisons: When performing multiple comparisons between proportions (e.g., comparing several different treatments), adjust the significance level to account for the increased chance of finding a false positive. Methods like Bonferroni correction can help manage this issue.
- Data Quality: The accuracy of the confidence interval depends entirely on the quality of the data. Inaccurate or biased data will lead to unreliable results.
- Causation vs. Correlation: A statistically significant difference between two proportions does not necessarily imply a causal relationship. Other factors may be influencing the observed difference.
Practical Applications of Two-Proportion Confidence Intervals
The applications of two-proportion confidence intervals are extensive across various disciplines:
- A/B Testing: In web development and marketing, A/B testing compares two different versions of a website or advertisement to determine which performs better. A confidence interval helps quantify the difference in conversion rates or click-through rates.
- Clinical Trials: In medical research, clinical trials often compare the effectiveness of two different treatments. Confidence intervals help assess the difference in treatment success rates.
- Survey Research: When analyzing survey data, confidence intervals can be used to compare proportions across different demographic groups or to assess changes in proportions over time.
- Quality Control: In manufacturing, confidence intervals can be used to monitor the proportion of defective products.
Reporting the Results
When reporting the results of a two-proportion confidence interval analysis, be sure to include:
- The point estimate: The difference between the two sample proportions (p̂₁ - p̂₂).
- The confidence interval: The lower and upper bounds of the interval.
- The confidence level: The chosen confidence level (e.g., 95%).
- The sample sizes: The number of observations in each group (n₁ and n₂).
- The method used: Specify the method used to calculate the confidence interval (e.g., z-interval, Wilson score interval).
- Contextual Interpretation: Clearly explain the practical implications of the results in the context of the study or experiment.
Conclusion
A confidence interval calculator for two proportions is an invaluable tool for researchers, analysts, and anyone working with data that involves comparing two proportions. Understanding the principles behind the calculations, choosing the appropriate method, and interpreting the results correctly are crucial for drawing meaningful conclusions and making informed decisions. Always remember to consider the limitations of the analysis and present your findings clearly and accurately. By utilizing these principles and employing a reliable confidence interval calculator, you can significantly enhance the robustness and validity of your statistical analyses.
Latest Posts
Latest Posts
-
What Is The Difference Between Intermolecular And Intramolecular Forces
Apr 03, 2025
-
Where Is The Energy Stored In Glucose
Apr 03, 2025
-
Light Amplification By The Stimulated Emission Of Radiation
Apr 03, 2025
-
Octet Rule Violation Vs Wrong Electron Total
Apr 03, 2025
-
What Are The Three Points Of Cell Theory
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Confidence Interval Calculator For 2 Proportions . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
