Critical Value Of 99 Confidence Interval
Muz Play
Mar 29, 2025 · 6 min read
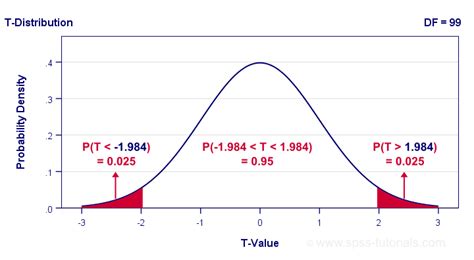
Table of Contents
The Critical Value of a 99% Confidence Interval: A Deep Dive
The concept of a confidence interval is fundamental in statistics, providing a range of values within which a population parameter is likely to fall with a certain degree of confidence. A 99% confidence interval, in particular, signifies a high level of certainty, indicating that if the same sampling procedure were repeated numerous times, 99% of the calculated intervals would contain the true population parameter. Understanding the critical value associated with this interval is crucial for accurate interpretation and application. This article will delve into the critical value of a 99% confidence interval, exploring its calculation, implications, and practical applications across various statistical contexts.
Understanding Confidence Intervals and Critical Values
Before diving into the specifics of a 99% confidence interval, let's establish a foundational understanding of the core concepts. A confidence interval is an estimated range of values that likely contains an unknown population parameter. This range is calculated from sample data and is accompanied by a confidence level, expressing the probability that the interval contains the true parameter.
The critical value, often denoted as z or t, is a crucial component in calculating the margin of error, which determines the width of the confidence interval. It represents the number of standard errors from the sample statistic needed to encompass the desired percentage of the sampling distribution. The critical value is directly linked to the chosen confidence level and the distribution used (typically the standard normal or t-distribution).
Calculating the Critical Value for a 99% Confidence Interval
The method for determining the critical value depends on whether you're using the standard normal distribution (z-distribution) or the t-distribution.
Using the Z-Distribution
The z-distribution is appropriate when the population standard deviation is known or the sample size is large (generally considered n ≥ 30). For a 99% confidence interval, you need to find the z-score that corresponds to the upper tail probability of 0.005 (1 - 0.99 = 0.01, divided by 2 for a two-tailed test). Consulting a z-table or using statistical software, you'll find that the critical value (z) is approximately 2.576.
This means that 99% of the area under the standard normal curve lies between -2.576 and +2.576 standard deviations from the mean.
Using the T-Distribution
The t-distribution is used when the population standard deviation is unknown and the sample size is small (n < 30). The t-distribution accounts for the additional uncertainty introduced by estimating the population standard deviation from the sample. The critical value for a 99% confidence interval using the t-distribution depends on the degrees of freedom (df), which is calculated as df = n - 1, where 'n' is the sample size.
To find the critical t-value, you'll need to consult a t-table or use statistical software, specifying the desired confidence level (99%) and the degrees of freedom. For example, with df = 10, the critical t-value is approximately 3.169. Note that as the degrees of freedom increase, the t-distribution approaches the z-distribution.
Implications of Using a 99% Confidence Interval
Opting for a 99% confidence interval, rather than a lower confidence level like 95%, has significant implications:
-
Wider Interval: A higher confidence level results in a wider confidence interval. This is because to ensure a higher probability of capturing the true population parameter, the margin of error needs to be larger, leading to a broader range of values.
-
Increased Precision vs. Confidence: While a 99% confidence interval offers greater confidence in containing the true parameter, it sacrifices precision. The wider interval provides a less precise estimate of the population parameter.
-
Sample Size Considerations: Achieving a 99% confidence interval often requires a larger sample size compared to a lower confidence level. This is because a larger sample size reduces the sampling error and allows for a narrower interval at the same confidence level, but a higher confidence level still demands more data.
-
Practical Significance: The increased confidence may not always outweigh the loss in precision. The practical implications of a wider interval should be considered in the context of the research question and the potential uses of the findings.
Applications of 99% Confidence Intervals Across Different Fields
The application of 99% confidence intervals extends across a wide array of fields, where high confidence in the estimation of parameters is crucial:
Medicine and Clinical Trials:
In clinical trials, researchers often use 99% confidence intervals to determine the effectiveness of new treatments or interventions. A 99% confidence interval provides a strong level of assurance that the observed effect is real and not due to chance.
Finance and Investment:
In financial modeling and risk assessment, 99% confidence intervals are utilized to estimate potential investment returns and assess the risk associated with different investment strategies. The high confidence level helps in mitigating the risk of significant losses.
Engineering and Quality Control:
In engineering and manufacturing, 99% confidence intervals are employed to assess the reliability and quality of products. This ensures that the product specifications meet the required standards with a very high degree of certainty.
Environmental Science:
Environmental studies often rely on 99% confidence intervals to estimate population sizes of endangered species or to quantify the impact of pollution on environmental variables. The high confidence level ensures robust conclusions.
Social Sciences:
Researchers in social sciences use 99% confidence intervals to analyze survey data and estimate population proportions with a high degree of accuracy. This allows for more reliable inferences about social trends and behaviors.
Choosing the Appropriate Confidence Level
The selection of an appropriate confidence level depends largely on the specific context and the consequences of making an incorrect inference. While a 99% confidence interval offers a high degree of certainty, it is crucial to consider the trade-off between confidence and precision.
In situations where the cost of an incorrect inference is high, such as in medical treatments or financial decisions, a higher confidence level may be justified. However, in other situations where a less precise estimate is acceptable, a lower confidence level may suffice. The research question, available resources (sample size), and potential impact of the findings should all be taken into account when determining the most appropriate confidence level.
Conclusion: The Importance of Critical Value in 99% Confidence Intervals
The critical value is a cornerstone in calculating a 99% confidence interval. Understanding its calculation and implications is essential for proper interpretation and application of confidence intervals across various fields. Remember to carefully consider the trade-off between confidence and precision when choosing the confidence level, always keeping the specific context and research objectives in mind. The choice of using a 99% confidence interval, while providing a high level of assurance, necessitates a thorough understanding of its implications and a justification for its selection in the context of the research problem at hand. The accuracy and reliability of the results depend critically on the correct selection and application of the appropriate critical value. Therefore, a thorough understanding of the underlying principles is crucial for drawing meaningful and robust conclusions from statistical analyses.
Latest Posts
Latest Posts
-
How To Find The Perpendicular Vector
Apr 01, 2025
-
What Are The Factors In An Experiment
Apr 01, 2025
-
What Is In The Cranial Cavity
Apr 01, 2025
-
Lab Skills Using A Graduated Cylinder
Apr 01, 2025
-
Which Molecules In Eukaryotic Cells Regulate Gene Expression
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Critical Value Of 99 Confidence Interval . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
