Definition Of Uniform Motion In Physics
Muz Play
Mar 27, 2025 · 6 min read
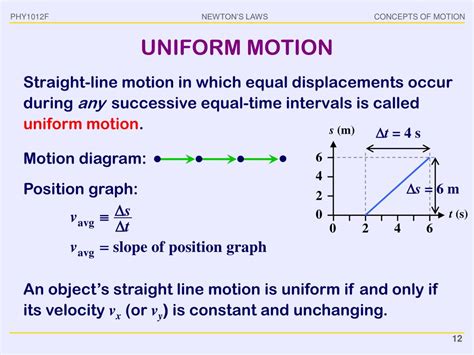
Table of Contents
Uniform Motion in Physics: A Comprehensive Guide
Uniform motion, also known as constant velocity motion, is a fundamental concept in classical mechanics. Understanding it is crucial for grasping more advanced topics in physics. This comprehensive guide will delve into the definition, characteristics, equations, examples, and significance of uniform motion. We will also explore its relationship with other concepts like acceleration and Newton's laws of motion.
Defining Uniform Motion
In physics, uniform motion refers to the movement of an object in a straight line at a constant speed. This means two key aspects remain unchanged throughout the motion:
- Direction: The object maintains a consistent direction; it doesn't change its course.
- Speed: The object's speed remains constant; it doesn't speed up or slow down.
It's crucial to distinguish between speed and velocity. Speed is a scalar quantity, representing only the magnitude of how fast an object is moving. Velocity, on the other hand, is a vector quantity, incorporating both magnitude (speed) and direction. Therefore, uniform motion implies a constant velocity vector. Any change in either speed or direction signifies the absence of uniform motion.
Key Characteristics of Uniform Motion:
-
Constant Velocity: This is the defining characteristic. The object's velocity vector remains unchanged over time.
-
Straight-line Path: The object follows a straight trajectory. Any deviation from a straight line indicates non-uniform motion.
-
Zero Acceleration: Since acceleration is the rate of change of velocity, a constant velocity means zero acceleration. This is a direct consequence of uniform motion.
-
Predictable Position: The position of the object at any given time can be precisely predicted using simple equations of motion.
Equations of Uniform Motion
The simplicity of uniform motion allows for straightforward mathematical description. The primary equation governing uniform motion is:
s = ut + c
Where:
- s represents the final displacement (distance covered in a specific direction) of the object.
- u is the initial velocity (constant in this case).
- t represents the time elapsed.
- c represents the initial displacement (position at t=0). Often, c=0 if the initial position is considered the origin.
This equation is a direct consequence of the definition of velocity as the rate of change of displacement: velocity = displacement/time. Since velocity is constant, the equation elegantly describes the object's displacement over time.
Graphical Representation of Uniform Motion
Uniform motion exhibits a characteristically linear relationship between displacement and time when plotted graphically. The graph of displacement (s) against time (t) will always be a straight line with a slope equal to the velocity (u). This linear relationship is a key visual indicator of uniform motion. The steeper the slope, the higher the velocity.
Examples of (Near) Uniform Motion
While perfectly uniform motion is theoretically ideal, several real-world scenarios approximate it closely:
-
A car traveling at a constant speed on a straight highway: While the driver might adjust the speed slightly, maintaining a relatively constant speed and direction for a reasonable period is achievable.
-
A puck sliding across frictionless ice: In an idealized frictionless environment, a puck would slide indefinitely at a constant velocity. This illustrates the concept well, though perfectly frictionless surfaces don't exist in reality.
-
A satellite orbiting Earth at a constant altitude: While the satellite is constantly changing direction (following a circular path), its speed remains relatively constant. This is often simplified as uniform circular motion (although not strictly uniform motion as defined above because of the changing direction).
-
An object in freefall (in a vacuum): In the absence of air resistance, an object falling freely under gravity would experience constant acceleration (due to gravity). However, if we were to consider horizontal motion in a vacuum, an object with initial horizontal velocity would exhibit uniform motion.
These examples highlight that uniform motion serves as a valuable model for understanding real-world situations, even if they never perfectly match the theoretical ideal.
Distinguishing Uniform Motion from Non-Uniform Motion
It's crucial to be able to differentiate uniform motion from its counterpart. Non-uniform motion occurs when either the speed or direction (or both) of the object changes. This implies the presence of acceleration. Several scenarios exemplify non-uniform motion:
-
A car accelerating from a stop: The speed is increasing, hence it's non-uniform motion.
-
A ball thrown vertically upwards: The ball's speed decreases as it goes up, then increases as it comes down, making it non-uniform motion.
-
A car taking a turn: Even at constant speed, the changing direction implies non-uniform motion.
-
A projectile's motion: The projectile's trajectory is curved; both speed and direction change throughout its flight.
The Role of Acceleration in Uniform and Non-Uniform Motion
Acceleration is the rate of change of velocity. In uniform motion, acceleration is zero because the velocity remains constant. In non-uniform motion, acceleration is non-zero, indicating a change in either speed, direction, or both.
The relationship between acceleration and velocity is expressed by the equation:
a = (v - u) / t
Where:
- a represents the acceleration.
- v is the final velocity.
- u is the initial velocity.
- t is the time interval.
In uniform motion, v = u, resulting in a = 0.
Newton's Laws and Uniform Motion
Newton's first law of motion, also known as the law of inertia, is intrinsically linked to uniform motion. The law states that an object at rest stays at rest and an object in motion stays in motion with the same speed and in the same direction unless acted upon by an unbalanced force. This directly implies that uniform motion persists in the absence of net external forces.
Any change in motion, signifying non-uniform motion, requires a net force acting on the object, as described by Newton's second law (F = ma). In the case of uniform motion, the net force is zero.
Limitations of the Uniform Motion Model
While a useful simplification, the uniform motion model has limitations:
-
Idealized Conditions: It assumes ideal conditions such as frictionless surfaces or absence of air resistance, which rarely occur in the real world.
-
Limited Applicability: It only applies to objects moving in a straight line at a constant speed. Many real-world movements are far more complex.
-
Neglect of Other Forces: The model often neglects other forces that might be present, such as gravitational forces or magnetic forces, which can influence motion.
Advanced Concepts Related to Uniform Motion
Understanding uniform motion provides a solid foundation for understanding more complex concepts:
-
Relative Motion: The velocity of an object can be different relative to different observers. Understanding relative velocity is crucial in situations where multiple objects are in motion.
-
Uniform Circular Motion: Although not strictly uniform motion (due to changing direction), uniform circular motion shares similarities, involving constant speed but varying velocity due to the change in direction.
-
Projectile Motion: While non-uniform, projectile motion can be analyzed by resolving it into horizontal (often uniform) and vertical (uniformly accelerated) components.
Conclusion
Uniform motion, despite its simplicity, serves as a crucial building block in classical mechanics. By understanding its definition, characteristics, equations, and limitations, we can better appreciate the complexities of more realistic movement. Its relationship with Newton's laws, acceleration, and other motion concepts highlights its importance in the broader field of physics. While real-world applications seldom perfectly reflect uniform motion, its theoretical framework provides a valuable foundation for analyzing and predicting the behavior of objects in motion. The ability to distinguish uniform motion from non-uniform motion is a critical skill for any student of physics. Mastering this fundamental concept paves the way for a deeper understanding of more intricate and dynamic forms of motion.
Latest Posts
Latest Posts
-
Adding Rational Expressions With Unlike Denominators
Mar 30, 2025
-
Where Protons And Neutrons Are Located
Mar 30, 2025
-
How To Find The Extinction Coefficient
Mar 30, 2025
-
Why Lipids Are Not Soluble In Water
Mar 30, 2025
-
Adding Integers With The Same Sign
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about Definition Of Uniform Motion In Physics . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
