Determine The Force In Each Member Of Truss
Muz Play
Mar 30, 2025 · 6 min read
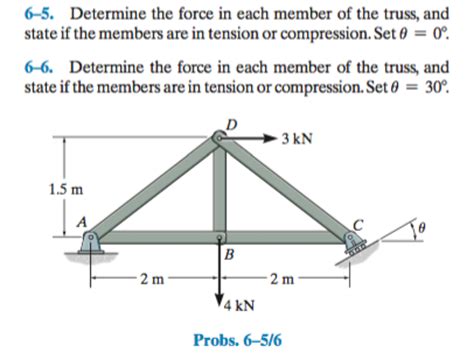
Table of Contents
Determining the Force in Each Member of a Truss: A Comprehensive Guide
Trusses are fundamental structural elements found in bridges, roofs, and towers. Their efficiency stems from the triangulation of members, which allows them to distribute loads effectively. Understanding how to determine the force in each member of a truss is crucial for engineers and designers ensuring structural integrity and safety. This comprehensive guide will walk you through various methods to achieve this, from fundamental concepts to advanced techniques.
Understanding Truss Basics
Before delving into force calculations, let's establish a strong foundation in truss terminology and behavior.
What is a Truss?
A truss is a structure composed of slender members interconnected at their ends to form a rigid framework. These members are typically straight and only subjected to axial forces – either tension (pulling force) or compression (pushing force). The connections, or joints, are assumed to be pin joints, meaning they allow rotation but not significant bending moments. This simplification is crucial for the analysis methods we’ll discuss.
Types of Trusses
Numerous truss configurations exist, each with its own characteristics and applications. Common types include:
- Simple Trusses: These are basic trusses easily analyzed using simple methods. Examples include the Pratt, Howe, and Warren trusses.
- Compound Trusses: These are larger trusses formed by combining simple trusses. Analysis requires breaking them down into smaller, simpler units.
- Complex Trusses: These have irregular configurations, making analysis more challenging and often requiring computer-aided engineering (CAE) software.
Assumptions in Truss Analysis
Several simplifying assumptions underpin most truss analyses:
- Members are straight and slender: This assumption neglects the effects of bending and shear.
- Joints are pin-connected: This assumption ensures that only axial forces exist in members.
- Loads are applied at the joints: This simplifies analysis by avoiding distributed loads along the members.
- Self-weight of the members is negligible: This assumption simplifies calculations, especially for lighter trusses.
Methods for Determining Member Forces
Several methods exist for calculating the forces within a truss. The choice of method depends on the complexity of the truss and the desired level of accuracy.
Method 1: Method of Joints
This method is suitable for simpler trusses and relies on equilibrium equations at each joint. For each joint, two equilibrium equations can be written:
- ΣFx = 0 (Sum of horizontal forces equals zero)
- ΣFy = 0 (Sum of vertical forces equals zero)
Steps:
- Draw a free body diagram (FBD) of the entire truss. This diagram shows all external forces acting on the truss.
- Identify the support reactions. This involves applying equilibrium equations to the entire truss structure (ΣFx = 0, ΣFy = 0, ΣM = 0).
- Start at a joint with only two unknowns. This often involves a joint with only one or two members connected to it.
- Apply the equilibrium equations (ΣFx = 0, ΣFy = 0) to solve for the unknown member forces.
- Proceed to adjacent joints, solving for unknowns until all member forces are determined.
- Note that a positive force indicates tension, while a negative force indicates compression.
Advantages: Relatively straightforward for simpler trusses.
Disadvantages: Can become cumbersome for complex trusses with many members and joints.
Method 2: Method of Sections
This method is particularly efficient for finding the forces in specific members within a larger truss. It involves cutting through the truss with an imaginary section and analyzing the equilibrium of one of the resulting segments.
Steps:
- Draw a free body diagram (FBD) of the entire truss.
- Identify the support reactions.
- Pass a section through the members whose forces you want to determine. The section should cut through no more than three members whose forces are unknown.
- Isolate one of the resulting segments.
- Apply the equilibrium equations (ΣFx = 0, ΣFy = 0, ΣM = 0) to solve for the unknown member forces.
- Note that a positive force indicates tension, while a negative force indicates compression.
Advantages: Efficient for determining forces in specific members without solving for all member forces.
Disadvantages: Not suitable for determining forces in all members simultaneously.
Method 3: Graphical Method
This method uses vector diagrams to determine member forces. While less common with the advent of computational methods, understanding this approach can provide valuable insights into force distribution within the truss.
Steps:
- Draw a vector diagram representing the external forces on the truss.
- Draw a polygon of forces for each joint, with each side representing a member force.
- The length and direction of each vector represent the magnitude and direction of the member force.
Advantages: Provides a visual representation of force distribution.
Disadvantages: Can be less accurate than analytical methods, particularly for complex trusses.
Method 4: Computer-Aided Engineering (CAE) Software
For complex trusses with numerous members, Computer-Aided Engineering (CAE) software is often the most efficient and accurate method. These programs use matrix methods to solve for member forces, handling complex geometries and loading conditions effectively.
Advantages: Handles complex trusses efficiently and accurately.
Disadvantages: Requires access to specialized software.
Illustrative Example: Method of Joints
Let's consider a simple truss to illustrate the Method of Joints:
Imagine a simple truss with a horizontal span of 6 meters and a vertical height of 3 meters. The truss is supported by a pin joint at the left end and a roller support at the right end. A vertical load of 10 kN is applied at the center joint.
Steps:
-
Calculate Support Reactions: Using equilibrium equations, we find the vertical reaction at the pin support (Ay) is 5 kN and the vertical reaction at the roller support (By) is 5 kN.
-
Joint A: We start with joint A, where we know Ay (5 kN) and two unknown member forces (FA and FB). Applying ΣFx = 0 and ΣFy = 0, we can solve for FA and FB.
-
Joint B: Next, consider Joint B, with the known forces FB and the unknown forces FC and FD. Again, applying ΣFx = 0 and ΣFy = 0, we solve for FC and FD.
-
Joint C: Repeat the process for joint C, which will have known forces FC and FD and unknown forces FE. Solving the equations gives FE.
-
Repeating process: The same process would be carried out on the remaining joints to find all the member forces.
Important Considerations
- Units: Always ensure consistent units throughout your calculations.
- Sign Convention: Establish a clear sign convention (e.g., positive for tension, negative for compression) and maintain consistency.
- Accuracy: Use appropriate significant figures in your calculations.
- Redundancy: Ensure the truss is statically determinate – meaning the number of unknowns equals the number of equilibrium equations. If a truss is statically indeterminate, more advanced methods, such as the Force Method or Displacement Method, are required.
Conclusion
Determining the force in each member of a truss is a fundamental task in structural engineering. The choice of method depends on the complexity of the truss and the specific information required. While simpler trusses can be analyzed effectively using the Method of Joints or Method of Sections, more complex structures necessitate the use of CAE software. Understanding these methods and applying them correctly ensures the design of safe and efficient structures. Remember that careful consideration of assumptions, accurate calculations, and proper interpretation of results are critical for structural integrity. This comprehensive guide provides a strong foundation for anyone seeking to master truss analysis.
Latest Posts
Latest Posts
-
What Is The Electron Configuration For Ne
Apr 01, 2025
-
Difference Between E1 And E2 Reaction
Apr 01, 2025
-
Journal Entry To Issue Common Stock
Apr 01, 2025
-
Real Life Examples Of Linear Equations In Two Variable
Apr 01, 2025
-
What Does An Mean In Arithmetic Sequences
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Determine The Force In Each Member Of Truss . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
