Equation Of A Cone In 3d
Muz Play
Mar 28, 2025 · 6 min read
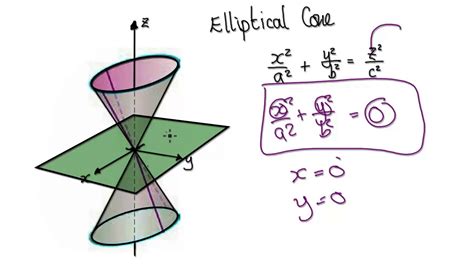
Table of Contents
The Equation of a Cone in 3D: A Comprehensive Guide
The equation of a cone in 3D might seem intimidating at first, but with a structured approach, understanding its derivation and applications becomes significantly easier. This comprehensive guide breaks down the concept, exploring different forms of the equation and its practical uses.
Understanding the Geometry of a Cone in 3D
Before diving into the equations, let's solidify our understanding of the cone's geometry. A cone in three-dimensional space is a three-dimensional geometric shape that tapers smoothly from a flat base (frequently, though not necessarily, circular) to a point called the apex or vertex. Key features include:
- Apex (Vertex): The single point at the top of the cone.
- Base: The flat surface at the bottom of the cone. While often circular, the base can be elliptical or any other closed curve.
- Axis: The straight line passing through the apex and the center of the base.
- Slant Height: The distance from any point on the base circumference to the apex.
- Height: The perpendicular distance from the apex to the base.
Understanding these elements is crucial for deriving and interpreting the equations.
Deriving the Equation of a Cone
The most common form of the cone equation is derived using the distance formula and the concept of a cone's half-angle. Let's consider a cone with its apex at the origin (0, 0, 0) and its axis aligned with the z-axis. Let 'α' be the half-angle of the cone (the angle between the axis and the slant height).
Any point (x, y, z) on the cone's surface satisfies the following relationship:
The distance from the point (x, y, z) to the z-axis is √(x² + y²). This represents the radius of the circular cross-section at height z. The ratio of this radius to the height z is equal to the tangent of the half-angle α:
tan(α) = √(x² + y²) / z
Rearranging this equation, we get the standard equation of a cone:
z = ±√(x² + y²) / tan(α)
Alternatively, we can express this equation using the relationship between the height and the slant height. This can be expressed in a more concise form:
x² + y² = z² tan²(α)
This equation defines a right circular cone with its apex at the origin. The ± sign accounts for the double cone (a cone extending above and below the apex). If we consider only the top half of the cone, we omit the negative solution.
Variations and Generalizations of the Cone Equation
The equation derived above represents a specific case: a right circular cone with its apex at the origin and its axis along the z-axis. We can generalize this to encompass more complex scenarios:
1. Cone with Apex at (x₀, y₀, z₀)
If the apex is shifted to a point (x₀, y₀, z₀), the equation becomes:
(x - x₀)² + (y - y₀)² = (z - z₀)² tan²(α)
This simply translates the origin to the new apex coordinates.
2. Cone with an Arbitrary Axis
For cones with axes not aligned with the z-axis, the derivation becomes more complex, often involving rotation matrices. The equation will incorporate terms representing the direction cosines of the cone's axis. This is usually tackled using vector notation and linear algebra. The generalized equation will not have a simple, closed-form expression as the above equations.
3. Elliptical Cones
While the above equations describe circular cones, we can extend the concept to elliptical cones. The equation for an elliptical cone, with its apex at the origin and axes along the x and y axes, can be written as:
(x²/a²) + (y²/b²) = (z/c)²
where 'a' and 'b' represent the semi-major and semi-minor axes of the base ellipse, and 'c' relates to the cone's height and angle. A further generalization allows for an arbitrary orientation of the elliptical base.
Applications of the Cone Equation
The equation of a cone finds applications in various fields:
- Computer Graphics: Cone equations are fundamental to rendering 3D objects, creating realistic shadows, and implementing lighting effects.
- Engineering and Design: Cones are used extensively in structural design, especially in the analysis of stress and strain.
- Physics: Cone-shaped geometries appear in numerous physical phenomena, such as the modeling of light beams, shock waves, and acoustic propagation.
- Mathematics: Cone equations provide a platform for exploring advanced geometrical concepts, such as conic sections (parabolas, ellipses, hyperbolas), and vector calculus.
- Game Development: Cone-based collision detection techniques, such as sphere-cone collision or cone-cone collision, are commonly implemented in game engines to enhance realistic object interaction.
- Astronomy: The study of celestial objects often involves analyzing cone-shaped regions, such as light cones used in astrophysical simulations to model the propagation of light over vast distances.
Solving Problems Involving Cone Equations
Many problems involve finding specific points on the cone, determining intersection points with other surfaces, or calculating volumes and surface areas. Here's a brief overview of strategies for tackling such problems:
- Substitution: If you have a system of equations (for example, the equation of a cone and a plane), you can often solve it by substituting one equation into another.
- Parametric Equations: Representing the cone's surface using parametric equations can simplify calculations, especially for surface area and volume calculations. This utilizes parameters like angle and height to define points on the cone's surface.
- Vector Methods: For more complex problems involving cones with arbitrary axes or orientations, using vector techniques and transformations can be highly efficient.
- Numerical Methods: For very complex scenarios without analytical solutions, numerical techniques like iterative methods (Newton-Raphson) might be needed to approximate the solutions.
Advanced Topics
This section briefly touches on advanced concepts that build upon the foundation of cone equations:
- Dual Cones: These cones have two parts emanating from a central point.
- General Quadric Surfaces: Cones belong to a broader class of surfaces called quadric surfaces which can be represented by second-degree equations.
- Differential Geometry: This field studies the intrinsic properties of curves and surfaces, including cones, using calculus.
Conclusion
The equation of a cone in 3D, while appearing complex at first, is a fundamental concept with far-reaching applications across multiple disciplines. This guide provides a comprehensive understanding, covering different variations, applications, and problem-solving strategies. With practice and a solid grasp of the underlying geometry and algebra, you can confidently tackle problems involving cones in 3D space. Remember to carefully consider the specific context of the problem and choose the most appropriate method for solving it. Whether you're working in computer graphics, engineering, or pure mathematics, a deep understanding of the 3D cone equation will prove invaluable.
Latest Posts
Latest Posts
-
5 Blind Man And The Elephant
Mar 31, 2025
-
Which Statement Describes The Citric Acid Cycle
Mar 31, 2025
-
Why Do Plants Love Water In Bio Terms
Mar 31, 2025
-
Identifying The Important Intermolecular Forces In Pure Compounds
Mar 31, 2025
-
Why Does Km Increase In Competitive Inhibition
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Equation Of A Cone In 3d . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
