Even And Odd Properties Of Trig Functions
Muz Play
Apr 05, 2025 · 5 min read
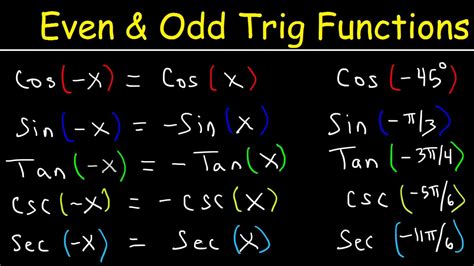
Table of Contents
Even and Odd Properties of Trigonometric Functions: A Comprehensive Guide
Trigonometric functions, the backbone of many mathematical and scientific applications, exhibit fascinating properties. Among these, the even and odd properties are particularly crucial for simplifying expressions, solving equations, and understanding their graphical representations. This comprehensive guide delves deep into the even and odd properties of sine, cosine, and tangent, along with their reciprocals, providing a robust understanding through definitions, proofs, and practical examples.
Understanding Even and Odd Functions
Before diving into the specifics of trigonometric functions, let's establish a clear understanding of what constitutes an even and an odd function. A function is considered:
-
Even: If f(-x) = f(x) for all x in the domain. Graphically, an even function is symmetric about the y-axis. Think of a parabola – it's perfectly mirrored on either side of the vertical axis.
-
Odd: If f(-x) = -f(x) for all x in the domain. Graphically, an odd function exhibits rotational symmetry about the origin. The function rotates 180° around (0,0) and remains unchanged. An example is the cubic function, y = x³.
Even and Odd Properties of the Core Trigonometric Functions
Now let's explore the even and odd nature of the fundamental trigonometric functions: sine, cosine, and tangent.
Cosine: An Even Function
The cosine function is an even function. This means:
cos(-x) = cos(x)
Proof:
This property stems directly from the definition of cosine in terms of the unit circle. Consider a point (x, y) on the unit circle corresponding to an angle x. The x-coordinate of this point represents cos(x). Now, consider the angle -x. This represents a reflection across the x-axis. The x-coordinate remains unchanged, hence cos(-x) equals cos(x). Alternatively, using the cosine series expansion, we can see that only even powers of x are present, confirming its even nature.
Sine: An Odd Function
The sine function is an odd function. This implies:
sin(-x) = -sin(x)
Proof:
Similar to the cosine proof, let's consider the unit circle. The y-coordinate of a point on the unit circle at angle x represents sin(x). Reflecting this point across the x-axis (representing the angle -x) changes the sign of the y-coordinate. Therefore, sin(-x) = -sin(x). The sine series expansion, containing only odd powers of x, also supports this.
Tangent: An Odd Function
The tangent function, defined as sin(x)/cos(x), is also an odd function:
tan(-x) = -tan(x)
Proof:
This can be easily proven using the properties of sine and cosine:
tan(-x) = sin(-x) / cos(-x) = (-sin(x)) / (cos(x)) = -tan(x)
Even and Odd Properties of Reciprocal Trigonometric Functions
The reciprocal trigonometric functions – secant (sec), cosecant (csc), and cotangent (cot) – also exhibit even and odd properties, directly inherited from their respective counterparts.
Secant: An Even Function
Secant, the reciprocal of cosine, is an even function:
sec(-x) = sec(x)
Proof: Since sec(x) = 1/cos(x), and cos(x) is even, its reciprocal, sec(x), must also be even.
Cosecant: An Odd Function
Cosecant, the reciprocal of sine, is an odd function:
csc(-x) = -csc(x)
Proof: As csc(x) = 1/sin(x), and sin(x) is odd, its reciprocal, csc(x), is also odd.
Cotangent: An Odd Function
Cotangent, the reciprocal of tangent, is an odd function:
cot(-x) = -cot(x)
Proof: Since cot(x) = 1/tan(x), and tan(x) is odd, its reciprocal, cot(x), is also odd.
Applications of Even and Odd Properties
The even and odd properties of trigonometric functions are invaluable in various mathematical contexts. Here are some key applications:
-
Simplifying Trigonometric Expressions: These properties allow for the simplification of complex trigonometric expressions. For instance, sin(-30°) can be directly simplified to -sin(30°) = -1/2.
-
Solving Trigonometric Equations: Understanding these properties helps in solving trigonometric equations more efficiently. For example, when encountering an equation like cos(x) = cos(-x), we can immediately conclude that this holds true for all x.
-
Graphing Trigonometric Functions: The even and odd properties dictate the symmetry of the graphs of these functions. Recognizing this symmetry significantly simplifies the process of graphing.
-
Calculus: These properties are crucial in calculus, especially in determining derivatives and integrals of trigonometric functions. They are used extensively in proving trigonometric identities and evaluating limits. Odd functions have a particularly simple definite integral from -a to a; it is always zero!
-
Physics and Engineering: Numerous applications in physics and engineering rely on trigonometric functions, making these properties essential tools for solving problems related to oscillations, waves, and rotations.
Practical Examples
Let's illustrate the applications with a few practical examples:
Example 1: Simplifying an Expression
Simplify the expression: sin(-θ) + cos(-2θ)
Solution:
Using the even and odd properties:
sin(-θ) + cos(-2θ) = -sin(θ) + cos(2θ)
Example 2: Solving a Trigonometric Equation
Solve the equation: sin(x) = -sin(30°)
Solution:
Using the odd property of sine:
sin(x) = -sin(30°) => sin(x) = sin(-30°)
Therefore, x = -30° + 360°k or x = 180° - (-30°) + 360°k = 210° + 360°k, where k is an integer.
Example 3: Calculus Application
Evaluate the definite integral: ∫<sub>-π</sub><sup>π</sup> sin(x) dx
Solution:
Since sin(x) is an odd function integrated over a symmetric interval [-π, π], the integral evaluates to 0.
Conclusion
The even and odd properties of trigonometric functions are fundamental concepts with far-reaching implications in mathematics, science, and engineering. Mastering these properties not only simplifies calculations but also provides deeper insights into the behavior and characteristics of trigonometric functions, empowering you to tackle more complex problems with greater efficiency and understanding. Remember to utilize these properties whenever possible to simplify expressions, solve equations, and analyze graphical representations for smoother, more efficient problem-solving.
Latest Posts
Latest Posts
-
Used To Help Substances Enter Or Exit The Cell Membrane
Apr 05, 2025
-
Verify That Is A Solution To The Differential Equation
Apr 05, 2025
-
Gaining Or Losing Electrons Is Called
Apr 05, 2025
-
How Sociology Differs From Other Social Sciences
Apr 05, 2025
-
Do Ionic Compounds Have High Boiling Points
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Even And Odd Properties Of Trig Functions . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
