Exterior Angle Of A Circle Formula
Muz Play
Apr 02, 2025 · 6 min read
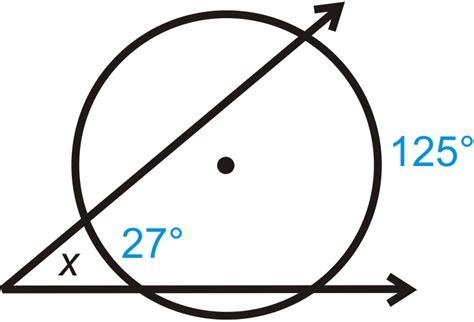
Table of Contents
Exterior Angle of a Circle: A Comprehensive Guide
The concept of an "exterior angle" typically refers to polygons. However, when we discuss circles, the term takes on a slightly different, yet equally fascinating, meaning. Understanding the exterior angle of a circle, while not a standard geometric term in the same way as, say, the central angle or inscribed angle, involves exploring related concepts that reveal deeper insights into circle geometry. This article delves into the intricacies of angles related to circles, explaining how various angles interact and providing a framework for understanding problems related to tangents, secants, and chords.
Understanding Angles Associated with Circles
Before directly addressing the "exterior angle," let's build a foundational understanding of the types of angles frequently encountered when working with circles. This foundation is crucial for grasping the nuances of angles formed outside the circle.
1. Central Angle
A central angle is an angle whose vertex is the center of the circle and whose sides are radii. The measure of a central angle is directly proportional to the length of the arc it subtends. In other words, a central angle of 60 degrees will subtend an arc that is 1/6th of the circle's circumference. This straightforward relationship is fundamental to many circle calculations.
2. Inscribed Angle
An inscribed angle is formed by two chords that share a common endpoint on the circle. The vertex of the inscribed angle lies on the circle, and the measure of the inscribed angle is half the measure of the central angle subtending the same arc. This relationship—inscribed angle = ½ central angle—is a cornerstone theorem in circle geometry.
3. Tangent-Secant Angle
A tangent is a line that intersects a circle at exactly one point (the point of tangency). A secant is a line that intersects a circle at two points. When a tangent and a secant intersect at a point outside the circle, they form angles. The measure of the angle formed by the tangent and the secant is half the difference of the intercepted arcs. This is a key relationship in solving problems involving tangents and secants.
4. Secant-Secant Angle
When two secants intersect outside a circle, they form angles whose measure is related to the intercepted arcs. Specifically, the measure of the angle formed by the two secants is half the difference of the measures of the intercepted arcs.
The Concept of "Exterior Angle" in Relation to Circles: Exploring Tangents and Secants
While there isn't a formally defined "exterior angle of a circle," the spirit of the question points to the angles formed outside the circle by intersecting lines, specifically tangents and secants. Therefore, we'll examine these angles and their relationships, clarifying how they relate to the arcs they intercept.
Let's consider the following scenarios:
Scenario 1: A Tangent and a Secant Intersect Outside the Circle
Imagine a circle with a tangent line intersecting a secant line at a point outside the circle. This creates two angles, one acute and one obtuse. Both these angles are related to the intercepted arcs within the circle.
The formula relating the exterior angle (formed by the tangent and secant) to the intercepted arcs is:
Exterior Angle = ½ (Measure of the major arc - Measure of the minor arc)
Scenario 2: Two Secants Intersect Outside the Circle
If two secants intersect outside the circle, they form four angles, but we're primarily interested in the exterior angle formed by the secants. The formula for this exterior angle is similar to the tangent-secant case:
Exterior Angle = ½ (Measure of the major arc - Measure of the minor arc)
Note that the "major arc" is the longer arc between the intersection points of the secants and the circle. The "minor arc" is the shorter arc between these same points.
Scenario 3: Two Tangents Intersect Outside the Circle
When two tangents intersect outside the circle, they create four angles (two pairs of vertical angles). The formula relating the exterior angle formed by the two tangents to the intercepted arcs is:
Exterior Angle = ½ (Measure of the major arc - Measure of the minor arc). In the case of two tangents, the major and minor arcs add up to 360 degrees.
Applications and Problem Solving
These formulas are essential for solving a variety of geometric problems involving circles. Here are a few examples:
Example 1: Finding an unknown arc measure
Given an exterior angle formed by a tangent and a secant, and the measure of one intercepted arc, we can solve for the measure of the other intercepted arc using the formula.
Example 2: Determining the angle between two tangents
Knowing the measures of the arcs intercepted by two tangents intersecting outside the circle, we can readily calculate the angle between the tangents.
Example 3: Solving for lengths of segments
While the formulas primarily focus on angles, they can indirectly contribute to solving problems involving the lengths of segments created by intersecting secants and tangents. This usually involves combining these angular relationships with other geometric theorems and properties.
Advanced Concepts and Extensions
The relationships we’ve explored can be extended and applied in more complex geometric scenarios. For example, we can consider cases with multiple tangents, secants, and chords intersecting within and outside the circle, generating a network of angles and arcs. These situations demand a systematic approach, breaking down the problem into smaller, more manageable parts using the fundamental relationships described earlier.
Practical Applications in Real-World Scenarios
Understanding circle geometry, including these angular relationships, is crucial in various fields:
- Engineering and Architecture: Designing curved structures, calculating distances, and determining optimal angles.
- Cartography and Geography: Mapping curved surfaces of the earth, calculating distances and bearings.
- Computer Graphics and Animation: Creating realistic curves and circular movements in computer-generated images and animations.
- Physics and Astronomy: Modeling circular orbits, analyzing rotational motion, and calculating projectile trajectories.
Conclusion
While the term "exterior angle of a circle" isn't a standard geometric term, the concept points to the crucial role of angles formed by lines intersecting a circle outside its circumference, involving tangents and secants. Understanding the relationships between these exterior angles and the intercepted arcs is vital for effectively solving a wide array of geometric problems. Mastering these relationships strengthens your understanding of circle geometry and provides valuable tools applicable to diverse fields. Practice and careful application of these formulas are key to developing proficiency in solving geometric problems involving circles. Remember to always clearly identify the major and minor arcs when using the formulas to ensure accurate calculations. The core principle remains consistent: the exterior angle is always half the difference between the major and minor intercepted arcs. By diligently applying these principles, you can tackle complex geometric challenges involving circles with confidence.
Latest Posts
Latest Posts
-
Image Formation In A Plane Mirror
Apr 03, 2025
-
Us Air Force Tongue And Quill
Apr 03, 2025
-
The Coefficients In A Chemical Equation Represent The
Apr 03, 2025
-
How To Calculate The Gradient Of A Stream
Apr 03, 2025
-
What Does Insoluble Mean In Chemistry
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Exterior Angle Of A Circle Formula . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
