Exterior Angles Of A Circle Theorem
Muz Play
Apr 04, 2025 · 5 min read
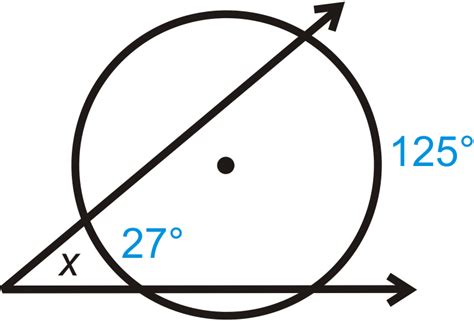
Table of Contents
Exterior Angles of a Circle Theorem: A Comprehensive Guide
The exterior angle theorem, a cornerstone of geometry, finds a powerful application in understanding the properties of circles. This article delves deep into the exterior angles of a circle theorem, exploring its proof, applications, and related concepts. We'll move beyond simple definitions and uncover the theorem's significance in solving complex geometrical problems.
Understanding the Theorem
The exterior angle theorem related to circles states: The measure of an angle formed by two secants, two tangents, or a secant and a tangent drawn from a point outside a circle is equal to half the difference of the measures of the intercepted arcs.
Let's break this down:
- Secant: A line that intersects a circle at two points.
- Tangent: A line that intersects a circle at exactly one point (the point of tangency).
- Intercepted Arcs: The arcs of the circle that lie between the points where the secants or tangents intersect the circle.
This theorem applies to three distinct scenarios:
-
Two Secants: Two secants drawn from an external point intercept two arcs. The exterior angle is half the difference between the larger and smaller intercepted arcs.
-
Two Tangents: Two tangents drawn from an external point intercept two arcs. The exterior angle is half the difference between the larger and smaller intercepted arcs (which in this case, one arc is a semicircle, and the other is the remaining portion).
-
One Secant and One Tangent: A secant and a tangent drawn from an external point intercept two arcs. The exterior angle is half the difference between the larger and smaller intercepted arcs.
Visual Representations
Imagine a circle with two secants drawn from a point P outside the circle. The secants intersect the circle at points A and B, and C and D respectively. The exterior angle at P is ∠APB. The intercepted arcs are arc AB and arc CD. According to the theorem, ∠APB = ½(arc CD - arc AB).
Similarly, for two tangents, imagine two tangents drawn from point P touching the circle at points A and B. The exterior angle is ∠APB. The intercepted arcs are the major arc AB and the minor arc AB. Again, ∠APB = ½(major arc AB - minor arc AB). Note that in the tangent case, one arc is effectively 360° minus the other.
Finally, for a secant and a tangent, let a secant intersect the circle at points A and B, and a tangent touch the circle at point C. The exterior angle formed is ∠P. The intercepted arcs are arc AC and arc BC. The theorem dictates that ∠P = ½(arc AC - arc BC).
Proof of the Theorem (Two Secants Case)
We'll demonstrate the proof for the case of two secants. The proofs for the other two cases follow a similar logic, incorporating slight adjustments.
1. Construction: Draw a line segment from point C to point B.
2. Angle Properties:
- ∠APB is the exterior angle we want to find.
- ∠ACB is an inscribed angle subtending arc AB. Thus, ∠ACB = ½(arc AB).
- ∠DBC is an inscribed angle subtending arc CD. Thus, ∠DBC = ½(arc CD).
3. Triangle Properties: In ΔPBC, the exterior angle ∠APB is equal to the sum of the two opposite interior angles:
∠APB = ∠PBC + ∠PCB
Substituting the values from step 2:
∠APB = ½(arc CD) + ½(arc AB)
4. Rearrangement: Now, let's consider the case where point B is not between A and P. In this case, we can rearrange the equation:
∠APB = ½ (arc CD - arc AB)
Applications and Problem Solving
The exterior angle theorem is a powerful tool for solving various geometry problems involving circles. Here are some examples:
Example 1: Find the measure of the angle formed by two tangents drawn from a point outside a circle, given that the intercepted arcs measure 100° and 260°.
Solution:
The exterior angle is half the difference of the intercepted arcs:
Exterior angle = ½ (260° - 100°) = 80°
Example 2: Two secants are drawn from a point outside a circle. The intercepted arcs measure 70° and 110°. Calculate the measure of the exterior angle.
Solution:
Exterior angle = ½ (110° - 70°) = 20°
Connecting to Other Theorems
The exterior angle theorem is intricately linked to other fundamental geometric concepts:
-
Inscribed Angle Theorem: This theorem states that an inscribed angle is half the measure of its intercepted arc. The proof of the exterior angle theorem utilizes the inscribed angle theorem.
-
Central Angle Theorem: A central angle is equal in measure to its intercepted arc. While not directly used in the proof, understanding the relationship between central and inscribed angles helps solidify the overall understanding.
-
Properties of Tangents: The theorem relies on the property that a tangent line is perpendicular to the radius drawn to the point of tangency.
Advanced Applications and Extensions
The exterior angle theorem's applications extend beyond simple angle calculations. It's crucial in:
-
Trigonometry: When combined with trigonometric functions, the theorem can be used to solve problems involving angles and distances in circles.
-
Calculus: The concepts underlying the theorem find applications in calculus when dealing with curves and tangents.
-
Computer Graphics: The theorem helps in creating accurate circle representations and calculating intersections in computer graphics applications.
Conclusion
The exterior angles of a circle theorem is a fundamental principle in geometry with far-reaching applications. Understanding its proof and its relationship to other theorems enhances problem-solving abilities and provides a solid foundation for more advanced mathematical concepts. By mastering this theorem, you gain a more profound understanding of the intricate relationships within circles and their properties. Remember to practice various problems to solidify your understanding and build your problem-solving skills. The more you apply this theorem, the more intuitive and useful it will become. This comprehensive guide provides a strong foundation for tackling more complex geometric challenges involving circles and their exterior angles.
Latest Posts
Latest Posts
-
Why Is Oil Necessary When Using The 100x Objective
Apr 04, 2025
-
Where Does Reduction Occur In An Electrolytic Cell
Apr 04, 2025
-
Analytical Balance Vs Top Loading Balance
Apr 04, 2025
-
Are Hydrogen Bonds Weak Or Strong
Apr 04, 2025
-
Is Brittle A Metal Nonmetal Or Metalloid
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Exterior Angles Of A Circle Theorem . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
