Formula Para Sacar Diametro De Un Circulo
Muz Play
Apr 01, 2025 · 4 min read
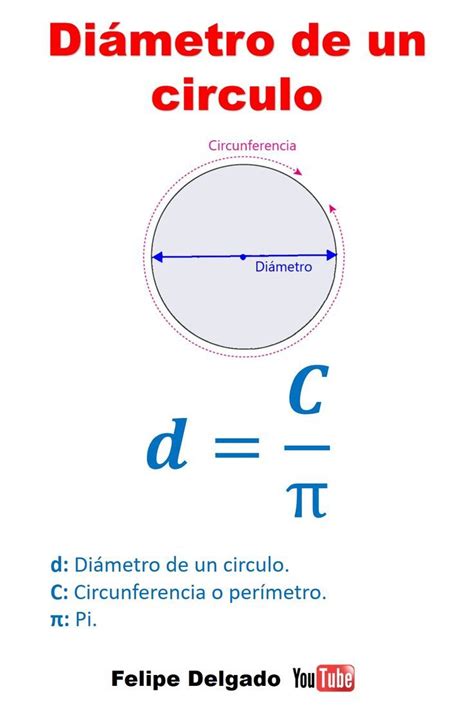
Table of Contents
Formulas to Calculate the Diameter of a Circle
Determining the diameter of a circle is a fundamental concept in geometry with wide-ranging applications across various fields, from engineering and architecture to computer graphics and data analysis. Understanding the different formulas and their appropriate usage is key to accurate calculations. This comprehensive guide will explore the various methods for calculating the diameter of a circle, emphasizing the relationship between diameter, radius, circumference, and area. We'll also delve into practical examples and consider scenarios where different formulas are most effective.
Understanding the Basics: Diameter, Radius, and Circumference
Before diving into the formulas, let's clarify the core terms:
-
Diameter: The diameter of a circle is the longest distance across the circle, passing through the center. It's a straight line segment that connects two points on the circle's circumference and bisects the circle.
-
Radius: The radius of a circle is the distance from the center of the circle to any point on its circumference. It's exactly half the length of the diameter.
-
Circumference: The circumference of a circle is the distance around the circle. It's the perimeter of the circle.
The relationship between these three elements is fundamental:
Diameter = 2 * Radius
Radius = Diameter / 2
Formula 1: Using the Radius
The simplest and most direct method to calculate the diameter is when the radius is known. As mentioned above:
Diameter (d) = 2 * Radius (r)
This formula is incredibly straightforward. If you know the radius, simply multiply it by two to obtain the diameter.
Example: A circle has a radius of 5 cm. Its diameter is 2 * 5 cm = 10 cm.
Formula 2: Using the Circumference
When the radius isn't readily available, but the circumference (C) is known, we can use the following formula, derived from the circumference formula:
Circumference (C) = π * Diameter (d)
To find the diameter, we rearrange the formula:
Diameter (d) = Circumference (C) / π
Where π (pi) is approximately 3.14159. Using a more precise value of π will yield a more accurate result. Many calculators have a dedicated π button for this purpose.
Example: A circle has a circumference of 25 cm. Its diameter is approximately 25 cm / 3.14159 ≈ 7.96 cm.
Formula 3: Using the Area
The area (A) of a circle is related to its diameter through the following formula:
Area (A) = π * (Radius (r))²
Since the radius is half the diameter, we can substitute r = d/2:
Area (A) = π * (d/2)² = (π * d²) / 4
Rearranging this formula to solve for the diameter gives us:
Diameter (d) = √(4 * Area (A) / π)
This formula is useful when the area of the circle is known. Remember to take the square root after calculating 4 * Area (A) / π.
Example: A circle has an area of 78.54 cm². Its diameter can be calculated as follows:
- 4 * 78.54 cm² / π ≈ 99.99 cm²
- √99.99 cm² ≈ 10 cm Therefore, the diameter is approximately 10 cm.
Choosing the Right Formula: A Practical Guide
The best formula to use depends on the information you have available:
-
If you know the radius: Use Diameter (d) = 2 * Radius (r). This is the simplest and most direct approach.
-
If you know the circumference: Use Diameter (d) = Circumference (C) / π. This is efficient when dealing with measurements of the circle's perimeter.
-
If you know the area: Use Diameter (d) = √(4 * Area (A) / π). This formula is particularly useful in situations where the area is a primary known value.
Applications Across Disciplines
The calculation of a circle's diameter is crucial in numerous fields:
-
Engineering: Designing circular components, calculating pipe diameters, and determining wheel sizes all rely on accurate diameter calculations.
-
Architecture: Creating circular structures, designing arches, and planning layouts frequently involve calculating diameters.
-
Manufacturing: Producing circular parts, such as bearings, gears, and disks, demands precise diameter measurements.
-
Computer Graphics: Generating circles and other circular shapes in computer-aided design (CAD) software and video games relies on these fundamental geometric calculations.
-
Data Analysis: Analyzing circular data sets, like in geographic information systems (GIS) or statistical analysis, often involves determining diameters of relevant circles.
-
Physics and Astronomy: Calculating the size of celestial bodies or modeling circular motion relies on understanding diameter and related properties.
Advanced Concepts and Considerations
While the basic formulas are sufficient for many applications, some advanced concepts deserve mention:
-
Error Propagation: When using measured values for radius, circumference, or area, it's essential to consider the potential errors in these measurements and how those errors propagate through the calculations, affecting the final diameter result.
-
Units of Measurement: Always maintain consistency in units of measurement throughout the calculation. If the radius is given in centimeters, the diameter will also be in centimeters.
-
Approximations: Remember that π is an irrational number, meaning its decimal representation goes on forever. Using approximations (like 3.14 or 3.14159) introduces a small degree of error, which is usually acceptable for most practical purposes.
Conclusion
Calculating the diameter of a circle is a foundational skill with far-reaching implications. Understanding the different formulas – using the radius, circumference, or area – enables accurate calculations in diverse scenarios. By choosing the appropriate formula and understanding the context of the problem, you can effectively determine the diameter and leverage this knowledge across a multitude of applications. Remember to always double-check your work and ensure consistency in your units of measurement for accurate results. Mastering these techniques is essential for success in various fields that rely heavily on geometrical principles.
Latest Posts
Latest Posts
-
2 Protons 2 Neutrons 2 Electrons
Apr 02, 2025
-
Is Channel Protein Active Or Passive
Apr 02, 2025
-
Is Aluminum A Metal Or Metalloid
Apr 02, 2025
-
Which Of These Occurs During Reproduction Choose 1 Answer
Apr 02, 2025
-
The Atrioventricular Av Valves Are Closed
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Formula Para Sacar Diametro De Un Circulo . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
