Free Body Diagram Of A Car
Muz Play
Mar 30, 2025 · 8 min read
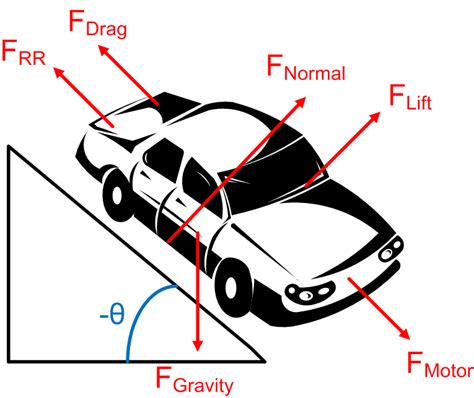
Table of Contents
Free Body Diagram of a Car: A Comprehensive Guide
Understanding the forces acting on a car is crucial for analyzing its motion, designing its components, and improving its performance. A powerful tool for visualizing and understanding these forces is the free body diagram (FBD). This comprehensive guide will delve into creating and interpreting FBDs for a car under various conditions, covering everything from simple scenarios to more complex situations involving acceleration, braking, and cornering.
What is a Free Body Diagram?
A free body diagram is a simplified visual representation of a system, showing all the forces acting on it. It isolates the object of interest (in this case, the car) from its surroundings and depicts each force as a vector, with its direction and magnitude clearly indicated. Creating an accurate FBD is essential for applying Newton's laws of motion to solve problems related to the car's dynamics.
Basic Components of a Car's Free Body Diagram
Before we delve into complex scenarios, let's establish the fundamental forces typically included in a car's FBD:
1. Gravity (Weight):
- Symbol: W (or Fg)
- Direction: Vertically downwards, towards the center of the Earth.
- Magnitude: Calculated as the mass of the car (m) multiplied by the acceleration due to gravity (g), i.e., W = mg.
2. Normal Force:
- Symbol: N
- Direction: Perpendicular to the surface the car is resting or moving on (typically upwards from the road surface).
- Magnitude: Equal in magnitude but opposite in direction to the component of the weight perpendicular to the surface. On a level surface, N = W.
3. Friction Force:
- Symbol: f
- Direction: Opposite to the direction of motion (or potential motion).
- Magnitude: Depends on the coefficient of friction (μ) between the tires and the road surface and the normal force (N), i.e., f = μN. This force is crucial for acceleration, braking, and cornering.
4. Thrust (Driving Force):
- Symbol: F<sub>t</sub>
- Direction: In the direction of motion (along the horizontal plane).
- Magnitude: Dependent on the engine's power and transmission. This force propels the car forward.
5. Drag Force (Air Resistance):
- Symbol: F<sub>d</sub>
- Direction: Opposite to the direction of motion.
- Magnitude: Dependent on the car's shape, speed, and air density. It increases significantly at higher speeds.
6. Rolling Resistance:
- Symbol: F<sub>r</sub>
- Direction: Opposite to the direction of motion.
- Magnitude: This force opposes the motion of the car due to deformation of the tires and the road surface. It’s relatively small compared to other forces at higher speeds but becomes significant at low speeds.
Creating a Free Body Diagram: Step-by-Step Guide
Let's illustrate how to create a FBD for a car in different scenarios:
Scenario 1: Car at Rest on a Level Surface
- Isolate the Car: Draw a simplified representation of the car as a box.
- Identify the Forces: The primary forces are gravity (W) acting downwards and the normal force (N) acting upwards. Since the car is at rest, the forces are balanced.
- Draw the Vectors: Draw arrows representing W and N. Make sure the length of the arrows reflects the relative magnitudes of the forces (in this case, they are equal). Label the arrows accordingly (W and N).
Resulting FBD: A simple diagram showing two equal and opposite vertical arrows representing W and N.
Scenario 2: Car Accelerating on a Level Surface
- Isolate the Car: Draw a simplified representation of the car.
- Identify the Forces: Gravity (W), Normal force (N), Thrust (F<sub>t</sub>), Friction (f) (although in this case, it is static friction, helping the wheels grip the road), and air resistance (F<sub>d</sub>).
- Draw the Vectors: Draw arrows for W and N (equal and opposite), a horizontal arrow representing the thrust force F<sub>t</sub> in the direction of motion, and a smaller horizontal arrow representing friction (f) opposite to the direction of motion. Include an arrow for air resistance, F<sub>d</sub>, which is relatively small at lower speeds and increases with speed.
- Consider Net Force: The net force in the horizontal direction (F<sub>net</sub>) is the difference between the thrust and the opposing forces (friction and air resistance). This net force is the reason for the car's acceleration.
Resulting FBD: A diagram showing vertical forces (W and N) and horizontal forces (F<sub>t</sub>, f, and F<sub>d</sub>), with F<sub>t</sub> being larger than the sum of f and F<sub>d</sub>.
Scenario 3: Car Braking on a Level Surface
- Isolate the Car: Draw a simplified representation of the car.
- Identify the Forces: Gravity (W), Normal force (N), Friction force (f), and air resistance (F<sub>d</sub>). Note that there is no thrust force in this scenario.
- Draw the Vectors: Similar to the acceleration scenario, draw arrows representing W and N. The braking force (f) is now acting in the opposite direction of the car's motion. Draw an arrow for air resistance, F<sub>d</sub>, opposite the direction of motion.
- Consider Net Force: The net force in the horizontal direction is the sum of friction and air resistance and is in the opposite direction of the car's motion, causing deceleration.
Resulting FBD: A diagram showing vertical forces (W and N) and horizontal forces (f and F<sub>d</sub>), both opposing the direction of motion.
Scenario 4: Car Cornering on a Level Surface
- Isolate the Car: Draw a simplified representation of the car.
- Identify the Forces: Gravity (W), Normal force (N), Friction force (f), and air resistance (F<sub>d</sub>). For cornering, friction acts as the centripetal force keeping the car on the curved path.
- Draw the Vectors: Draw W and N as usual. The friction force (f) is now directed towards the center of the curve, providing the centripetal force. Air resistance (F<sub>d</sub>) would act against the car's velocity.
- Consider Net Force: The net force in the horizontal direction is the friction force (f), pointing inwards towards the center of the curve.
Resulting FBD: A diagram showing vertical forces (W and N) and a horizontal force (f) pointing towards the center of the curve, indicating the centripetal force.
Scenario 5: Car on an Inclined Plane
When dealing with an inclined plane, you need to resolve the weight vector into components parallel and perpendicular to the plane.
- Isolate the Car: Draw the car on the inclined plane.
- Resolve Weight: Resolve the weight vector (W) into two components: one perpendicular to the plane (W<sub>⊥</sub>) and one parallel to the plane (W<sub>∥</sub>). W<sub>⊥</sub> acts downwards and W<sub>∥</sub> acts down the slope.
- Identify Other Forces: Include the normal force (N) perpendicular to the plane, friction force (f) up the plane (if the car is slowing down) or down the plane (if the car is speeding up), and possibly thrust or braking forces depending on the context.
- Draw the Vectors: Draw all the identified forces as vectors, labeling them clearly.
Resulting FBD: A diagram showcasing W<sub>⊥</sub> and W<sub>∥</sub>, N, and f, with their magnitudes and directions carefully considered in relation to the angle of inclination.
Advanced Considerations and Factors
While the above scenarios cover the basics, several factors can add complexity to a car's FBD:
- Aerodynamic forces: These forces become significant at higher speeds and involve lift and downforce, affecting the normal force and overall stability.
- Suspension forces: The suspension system exerts forces on the car's chassis, affecting the distribution of weight and the normal forces on the wheels.
- Engine torque: The engine torque is translated into a driving force at the wheels, but its distribution and impact on individual wheels can be complicated.
- Braking force distribution: The braking system distributes force to individual wheels, impacting the friction forces.
- Uneven road surfaces: These introduce additional forces and moments that complicate the analysis.
These advanced factors would require more sophisticated FBDs, potentially involving multiple free body diagrams for individual components of the car (wheels, suspension components etc) and employing techniques beyond basic Newtonian mechanics.
Applications of Car FBDs
Car FBDs are essential in various automotive engineering applications:
- Vehicle dynamics analysis: Understanding how a car handles in different conditions (acceleration, braking, cornering).
- Suspension design: Optimizing suspension systems to improve handling and ride comfort.
- Braking system design: Ensuring effective and safe braking performance.
- Tire design: Developing tires with appropriate grip characteristics.
- Safety system design: Designing safety features like airbags and seatbelts to mitigate the impact of collisions.
- Performance optimization: Improving fuel efficiency and acceleration by understanding forces affecting the car.
Conclusion
Creating and interpreting free body diagrams is a fundamental skill for anyone involved in automotive engineering or the study of vehicle dynamics. Understanding the forces acting on a car, even in simplified scenarios, provides valuable insight into its behaviour and allows for a quantitative analysis of its performance and safety. This guide has provided a step-by-step approach to construct FBDs for a car in various situations, covering basic and more advanced considerations. Mastering this skill will enhance your comprehension of automotive mechanics and open the door to more advanced analyses in the field. Remember that accuracy and clarity in your FBDs are paramount for obtaining meaningful results.
Latest Posts
Latest Posts
-
Difference Between Hypothesis Law And Theory
Apr 01, 2025
-
Is An Atom The Smallest Particle
Apr 01, 2025
-
Central Limit Theorem With Means Calculator
Apr 01, 2025
-
What Is The Difference Between Lactic Acid And Alcoholic Fermentation
Apr 01, 2025
-
Which Compound Is Produced During Regeneration
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Free Body Diagram Of A Car . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
