Graphing Sine And Cosine Functions Worksheet
Muz Play
Mar 29, 2025 · 6 min read
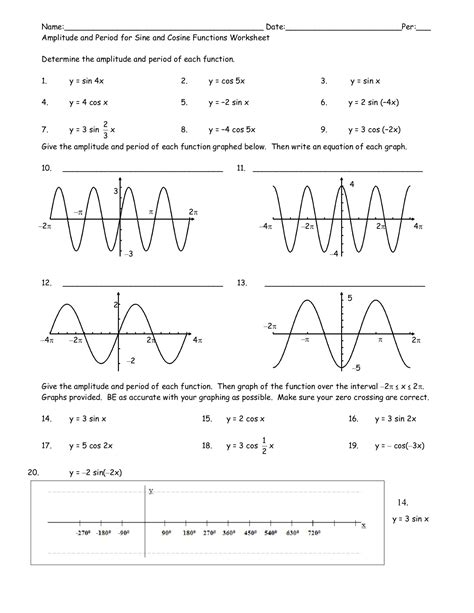
Table of Contents
Graphing Sine and Cosine Functions Worksheet: A Comprehensive Guide
This worksheet will delve into the fascinating world of graphing sine and cosine functions. We'll explore the key characteristics of these trigonometric functions, understand how to manipulate their graphs using various transformations, and ultimately master the skill of accurately sketching these graphs. This guide serves as a companion to any worksheet focusing on graphing sine and cosine functions, providing explanations, examples, and practice problems to solidify your understanding.
Understanding the Basic Sine and Cosine Graphs
Before diving into transformations, let's establish a firm grasp of the fundamental sine and cosine graphs.
The Sine Function: y = sin(x)
The sine function, denoted as y = sin(x), is a periodic function, meaning its graph repeats itself over a specific interval. This interval is called the period, and for the basic sine function, the period is 2π radians (or 360 degrees).
Key Characteristics of y = sin(x):
- Amplitude: The amplitude represents the height of the wave from the midline to its peak (or trough). For y = sin(x), the amplitude is 1.
- Period: As mentioned, the period is 2π. The graph completes one full cycle in this interval.
- Midline: The midline is the horizontal line about which the graph oscillates. For y = sin(x), the midline is y = 0 (the x-axis).
- x-intercepts: The graph intersects the x-axis at multiples of π (…,-2π, -π, 0, π, 2π,…).
- Maximum and Minimum Values: The maximum value is 1, and the minimum value is -1.
The Cosine Function: y = cos(x)
The cosine function, y = cos(x), is also a periodic function with a period of 2π. It's closely related to the sine function, with a key difference in its starting point.
Key Characteristics of y = cos(x):
- Amplitude: The amplitude is 1.
- Period: The period is 2π.
- Midline: The midline is y = 0.
- x-intercepts: The graph intersects the x-axis at odd multiples of π/2 (…,-3π/2, -π/2, π/2, 3π/2,…).
- Maximum and Minimum Values: The maximum value is 1, and the minimum value is -1.
Graph Transformations: Manipulating Sine and Cosine Graphs
Understanding transformations is crucial for graphing variations of the basic sine and cosine functions. These transformations involve changes in amplitude, period, phase shift (horizontal shift), and vertical shift.
Amplitude Changes: y = A sin(x) and y = A cos(x)
The value of 'A' determines the amplitude. If |A| > 1, the graph is vertically stretched, increasing the amplitude. If 0 < |A| < 1, the graph is vertically compressed, decreasing the amplitude. A negative value of A reflects the graph across the x-axis.
Example: y = 3sin(x) has an amplitude of 3. y = -0.5cos(x) has an amplitude of 0.5 and is reflected across the x-axis.
Period Changes: y = sin(Bx) and y = cos(Bx)
The value of 'B' affects the period. The period of y = sin(Bx) and y = cos(Bx) is given by (2π)/|B|. If |B| > 1, the period is compressed (graph becomes narrower). If 0 < |B| < 1, the period is stretched (graph becomes wider).
Example: y = sin(2x) has a period of π. y = cos(x/2) has a period of 4π.
Phase Shift (Horizontal Shift): y = sin(x - C) and y = cos(x - C)
The value of 'C' causes a horizontal shift. A positive value of C shifts the graph to the right, while a negative value shifts it to the left. This shift is often referred to as the phase shift.
Example: y = sin(x - π/2) is the same as y = cos(x). The sine graph is shifted π/2 units to the right, resulting in the cosine graph.
Vertical Shift: y = sin(x) + D and y = cos(x) + D
The value of 'D' causes a vertical shift. A positive value of D shifts the graph upwards, while a negative value shifts it downwards. The midline of the graph becomes y = D.
Example: y = cos(x) + 2 shifts the cosine graph 2 units upwards. The midline becomes y = 2.
Combining Transformations
Often, you'll encounter functions that involve multiple transformations. To graph these, apply the transformations sequentially:
- Vertical Stretch/Compression (A): Adjust the amplitude.
- Period Change (B): Adjust the period.
- Phase Shift (C): Shift horizontally.
- Vertical Shift (D): Shift vertically.
Example: Graph y = 2sin(3x - π) + 1
- Amplitude: 2
- Period: (2π)/3
- Phase Shift: π/3 (to the right, because we rewrite the equation as y = 2sin(3(x - π/3)) +1)
- Vertical Shift: 1 (upwards)
Practice Problems
Let's solidify your understanding with some practice problems:
- Graph y = 4cos(x/2)
- Graph y = -sin(2x + π)
- Graph y = 1/2 sin(x - π/4) - 1
- Determine the amplitude, period, phase shift, and vertical shift of y = -3cos(πx + 2π) + 4
- Write the equation of a sine function with an amplitude of 2, a period of 4π, a phase shift of π/2 to the left, and a vertical shift of 3 units down.
- Sketch the graph of y = 2cos(x) and y = 2cos(x - π/2) on the same axes and compare their similarities and differences. Explain why they are related.
- Explain how the graphs of y = sin x and y = cos x are related. Can one be obtained from the other through transformations? If so, how?
- Consider the graph of y = A sin(Bx - C) + D. Describe how changing each of the constants A, B, C, and D affects the graph.
Advanced Topics: Inverse Trigonometric Functions and Applications
Beyond basic graphing, exploring inverse trigonometric functions and real-world applications can greatly deepen your understanding. Inverse functions, such as arcsin, arccos, and arctan, allow us to find the angle given a trigonometric ratio.
Real-world applications of sine and cosine functions are abundant:
- Modeling oscillations: Simple harmonic motion (like a pendulum or spring) is modeled using sine and cosine functions.
- Sound waves: Sound waves are also described using these functions, with amplitude relating to loudness and frequency relating to pitch.
- Light waves: Similar to sound, light waves exhibit wave-like behavior modeled by sine and cosine functions.
- Tidal patterns: The rise and fall of tides can be approximated using trigonometric functions.
By mastering the fundamentals of graphing sine and cosine functions and exploring their applications, you'll not only improve your mathematical skills but also gain valuable insights into how these functions describe the world around us. This comprehensive guide, coupled with diligent practice, will equip you with the necessary tools to excel in this important area of mathematics. Remember to utilize online resources and consult textbooks for further in-depth study and additional practice problems.
Latest Posts
Latest Posts
-
Political Map Of North Africa And Southwest Asia
Mar 31, 2025
-
Work Is The Integral Of Force
Mar 31, 2025
-
Is Water A Reactant Or Product
Mar 31, 2025
-
Four Ways To Represent A Function
Mar 31, 2025
-
What Is The Functional Unit Of Heredity
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Graphing Sine And Cosine Functions Worksheet . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
