How To Calculate Interest On A Note Payable
Muz Play
Apr 06, 2025 · 5 min read
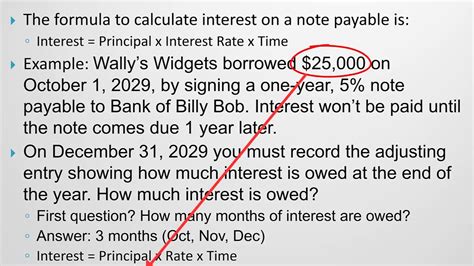
Table of Contents
How to Calculate Interest on a Note Payable: A Comprehensive Guide
Understanding how to calculate interest on a note payable is crucial for both businesses and individuals. Notes payable are formal written promises to repay a borrowed amount, and the interest represents the cost of borrowing that money. This comprehensive guide will walk you through the various methods of calculating interest, explore different types of notes, and offer practical examples to solidify your understanding.
Understanding Notes Payable
Before diving into the calculations, let's clarify what a note payable is. A note payable is a short-term or long-term liability representing a formal promise to repay a debt. These notes usually specify:
- Principal: The original amount borrowed.
- Interest Rate: The percentage charged on the principal. This rate can be fixed or variable.
- Maturity Date: The date when the principal and interest are due.
- Payment Terms: How the debt will be repaid (e.g., lump sum, installments).
The interest charged is compensation for the lender providing the funds. The calculation of this interest depends on several factors, including the interest rate, the principal amount, and the time period.
Methods for Calculating Interest on a Note Payable
Several methods exist for calculating interest on a note payable. The most common are:
1. Simple Interest
Simple interest is calculated only on the principal amount of the loan. It's the simplest method and is often used for short-term notes. The formula is:
Simple Interest = Principal x Interest Rate x Time
Where:
- Principal: The original amount borrowed.
- Interest Rate: The annual interest rate (expressed as a decimal).
- Time: The loan term in years (or a fraction thereof).
Example:
Suppose you borrow $10,000 at a 6% annual interest rate for 6 months. The simple interest calculation would be:
Simple Interest = $10,000 x 0.06 x (6/12) = $300
The total amount due at maturity would be $10,300 ($10,000 + $300).
When to use Simple Interest: Simple interest is best suited for short-term loans with a maturity of less than a year.
2. Compound Interest
Compound interest is calculated on the principal amount plus accumulated interest. This means that interest earned in one period is added to the principal, and subsequent interest calculations are based on this larger amount. This method typically leads to higher interest payments over time.
Calculating Compound Interest: The formula for compound interest is more complex:
A = P (1 + r/n)^(nt)
Where:
- A: The future value of the investment/loan, including interest.
- P: The principal investment amount (the initial deposit or loan amount).
- r: The annual interest rate (decimal).
- n: The number of times that interest is compounded per year.
- t: The number of years the money is invested or borrowed for.
Example:
Let's assume you borrow $10,000 at an annual interest rate of 6%, compounded monthly, for 2 years.
- P = $10,000
- r = 0.06
- n = 12 (monthly compounding)
- t = 2
A = $10,000 (1 + 0.06/12)^(12*2) = $11,268.25
The total interest paid would be $1,268.25 ($11,268.25 - $10,000).
When to use Compound Interest: Compound interest is used for longer-term loans where interest is compounded periodically (daily, monthly, quarterly, annually).
3. Discount Method
In some cases, especially with short-term notes, the interest is deducted upfront from the principal amount. This is known as the discount method. The borrower receives the principal amount minus the discounted interest, and at maturity, they repay the full principal amount.
Example:
A $10,000 note with a 6% annual discount rate for 6 months would have a discount of:
Discount = $10,000 x 0.06 x (6/12) = $300
The borrower receives $9,700 ($10,000 - $300) and repays $10,000 at maturity.
When to use Discount Method: The discount method is commonly used for short-term financing, such as short-term commercial loans.
4. Add-on Interest
This method calculates interest on the original principal amount and adds it to the loan's face value. The borrower then makes equal payments over the loan's term. This method often results in higher effective interest rates compared to other methods.
Example:
If you borrow $10,000 at 6% add-on interest for 2 years, the total interest is $1,200 ($10,000 x 0.06 x 2). The borrower repays $11,200 in equal installments over two years.
When to use Add-on Interest: While still used, add-on interest is becoming less common due to its potential for higher effective interest rates.
Factors Affecting Interest Calculations
Several factors can influence the interest calculations:
- Creditworthiness: Individuals or businesses with strong credit histories usually qualify for lower interest rates.
- Loan Term: Longer loan terms often lead to higher total interest payments, even at lower interest rates.
- Type of Loan: Different types of loans (e.g., mortgages, auto loans, business loans) have varying interest rates.
- Economic Conditions: Market interest rates can fluctuate based on macroeconomic factors, impacting the cost of borrowing.
Practical Applications and Considerations
- Accounting: Accurate interest calculation is essential for accurate financial reporting. Interest expense is recognized on the income statement, while notes payable are recorded as liabilities on the balance sheet.
- Budgeting: Understanding interest calculations allows individuals and businesses to budget for loan repayments effectively.
- Negotiating Loan Terms: Knowing how interest is calculated provides leverage when negotiating loan terms with lenders.
Beyond the Basics: Dealing with Irregular Periods
The examples above often assume convenient time periods. However, what if the loan term is not a whole number of years or months? To handle irregular periods, you need to use a fraction representing the portion of a year the loan is outstanding. For instance, 90 days would be expressed as 90/365 (or 90/360 depending on the convention used).
Example with Irregular Period:
A $5,000 loan at 8% annual interest for 75 days would be calculated as:
Interest = $5,000 x 0.08 x (75/365) ≈ $82.19
Conclusion
Calculating interest on a note payable accurately is critical for financial management. This guide covered the essential methods, including simple interest, compound interest, discount method, and add-on interest. Understanding these methods and their applications empowers individuals and businesses to make informed decisions related to borrowing and lending, ensuring financial transparency and responsible debt management. Remember to always clarify the terms of the note payable with the lender to ensure you are applying the correct calculation method and understanding your total liability.
Latest Posts
Latest Posts
-
What Does Composition Mean In Chemistry
Apr 07, 2025
-
Adolf Hitler Was A Great Leader
Apr 07, 2025
-
Identify The Resulting Resonance Structure Indicated By The Curved Arrows
Apr 07, 2025
-
How Do You Determine If A Function Has An Inverse
Apr 07, 2025
-
Can P Orbitals Form Sigma Bonds
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about How To Calculate Interest On A Note Payable . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
