How To Calculate Velocity From Flow Rate
Muz Play
Mar 29, 2025 · 6 min read
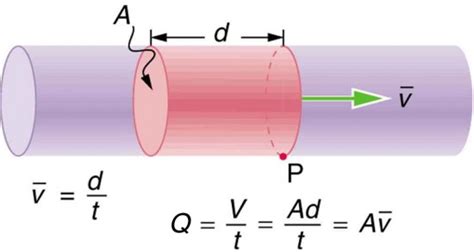
Table of Contents
How to Calculate Velocity from Flow Rate: A Comprehensive Guide
Understanding the relationship between flow rate and velocity is crucial in various fields, from fluid mechanics and hydraulics to environmental engineering and even healthcare. Whether you're designing a pipeline, analyzing blood flow, or studying river currents, knowing how to calculate velocity from flow rate is an essential skill. This comprehensive guide will explore this relationship in detail, providing clear explanations, practical examples, and considerations for different scenarios.
Understanding Flow Rate and Velocity
Before delving into the calculations, let's clearly define our key terms:
Flow Rate (Q): This represents the volume of fluid passing a given point per unit of time. Common units include liters per second (L/s), cubic meters per second (m³/s), gallons per minute (gpm), and cubic feet per second (cfs). Flow rate describes the quantity of fluid moving.
Velocity (v): This is a vector quantity representing the speed and direction of fluid movement at a specific point. It's typically measured in meters per second (m/s), feet per second (ft/s), or other units of distance per unit time. Velocity describes the speed of fluid movement.
The crucial difference lies in this: flow rate considers the total volume moving, while velocity focuses on the speed of the fluid at a particular location. They are intrinsically linked, and understanding this link is key to accurate calculations.
Calculating Velocity from Flow Rate: The Basic Formula
The fundamental relationship between flow rate (Q) and velocity (v) depends on the cross-sectional area (A) of the conduit through which the fluid is flowing. The formula is:
Q = A * v
Therefore, to calculate velocity (v) from flow rate (Q), we rearrange the formula:
v = Q / A
This simple equation forms the basis for all our calculations. However, the complexity arises in determining the appropriate cross-sectional area (A) for different flow geometries.
Calculating Velocity for Different Pipe Shapes
The accuracy of your velocity calculation hinges on correctly determining the cross-sectional area. Here's how to calculate the area for common shapes:
1. Circular Pipes:
Circular pipes are the most common type in many applications. The area (A) of a circle is calculated as:
A = π * r²
where:
- π is pi (approximately 3.14159)
- r is the radius of the pipe (half of the diameter)
Example: A circular pipe with a diameter of 10 cm (radius = 5 cm or 0.05 m) has a flow rate of 0.1 m³/s. What is the fluid velocity?
- Calculate the area: A = π * (0.05 m)² ≈ 0.00785 m²
- Calculate the velocity: v = 0.1 m³/s / 0.00785 m² ≈ 12.73 m/s
2. Rectangular Channels/Ducts:
For rectangular channels or ducts, the cross-sectional area is simply the product of the width (w) and height (h):
A = w * h
Example: A rectangular channel with a width of 2 meters and a height of 1 meter has a flow rate of 4 m³/s. What is the fluid velocity?
- Calculate the area: A = 2 m * 1 m = 2 m²
- Calculate the velocity: v = 4 m³/s / 2 m² = 2 m/s
3. Irregular Shapes:
For channels or conduits with irregular cross-sectional shapes, calculating the area becomes more complex. Accurate methods often involve:
- Direct Measurement: If possible, directly measure the area using techniques like planimetry (measuring the area on a drawing) or surveying techniques.
- Approximation: Approximate the irregular shape with simpler geometric shapes (rectangles, triangles) and sum their areas. This method introduces some error, but can be sufficiently accurate for many applications.
- Numerical Methods: Sophisticated numerical methods, often involving computer software, can provide highly accurate area estimations for complex shapes.
Considerations and Complications
While the basic formula v = Q / A provides a good starting point, several factors can influence the accuracy and applicability of the calculation:
1. Non-Uniform Flow:
The formula assumes uniform flow—that is, the velocity is constant across the entire cross-sectional area. In reality, this is rarely the case. Velocity profiles are often non-uniform, with higher velocities in the center of the pipe and lower velocities near the walls (due to friction). For more accurate velocity estimations in non-uniform flow scenarios, more advanced techniques such as computational fluid dynamics (CFD) might be necessary.
2. Compressible vs. Incompressible Fluids:
The formula applies most accurately to incompressible fluids (liquids), where the density remains relatively constant. For compressible fluids (gases), the density changes with pressure and temperature, significantly affecting the relationship between flow rate and velocity. More complex equations accounting for compressibility are needed in such cases.
3. Viscosity:
The viscosity (thickness) of the fluid influences its flow behavior and velocity profile. Highly viscous fluids will have slower velocities near the walls compared to less viscous fluids. For highly viscous fluids, advanced equations incorporating viscosity effects might be required.
4. Turbulence:
Turbulent flow adds complexity to velocity calculations. Turbulence is characterized by chaotic and irregular fluid motion, making the velocity distribution even more non-uniform than in laminar (smooth) flow. Accurate modelling of turbulent flow often requires advanced techniques like CFD.
Advanced Applications and Techniques
For more complex scenarios, advanced techniques and considerations are essential:
-
Pitot Tubes: These devices directly measure fluid velocity at a point by using the pressure difference between the stagnation point (where the fluid is brought to rest) and the surrounding flow. This provides a localized velocity measurement, which can be used to build a more comprehensive velocity profile.
-
Ultrasonic Flow Meters: These instruments employ ultrasonic waves to measure the velocity of fluids without directly contacting them. They are particularly useful for measuring velocity in pipes carrying hazardous or corrosive fluids.
-
Computational Fluid Dynamics (CFD): CFD uses numerical methods to solve fluid flow equations, providing highly detailed simulations of velocity profiles, pressure distributions, and other fluid properties. CFD is invaluable for complex geometries and flow conditions where analytical solutions are difficult or impossible to obtain.
-
Open Channel Flow: For open channels (rivers, canals), the calculation of velocity becomes more complex because the cross-sectional area can vary along the channel length, and the flow is significantly affected by gravity and the channel's geometry. Specialized formulas and techniques are used for these scenarios.
Conclusion: Mastering Velocity Calculations
Calculating velocity from flow rate is a fundamental skill in fluid mechanics and related fields. While the basic formula v = Q / A provides a valuable starting point, accurately determining the cross-sectional area and understanding the limitations of the formula (non-uniform flow, compressibility, viscosity, turbulence) are crucial for obtaining reliable results. As the complexity of the flow situation increases, more advanced techniques such as Pitot tubes, ultrasonic flow meters, and CFD become necessary for accurate velocity determination. By mastering these concepts and techniques, you'll be well-equipped to handle a wide range of fluid flow problems.
Latest Posts
Latest Posts
-
Motion Of Molecules Compared To Direction Of Motion Electromagnetic Waves
Apr 01, 2025
-
The Variance Is The Square Root Of The Standard Deviation
Apr 01, 2025
-
Easy Way To Find Common Multiples
Apr 01, 2025
-
What Is The Structural And Functional Unit Of The Kidney
Apr 01, 2025
-
Evolutionary Relationships Between Organisms Are Determined By
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about How To Calculate Velocity From Flow Rate . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
