How To Find Equation Of A Horizontal Line
Muz Play
Apr 06, 2025 · 5 min read
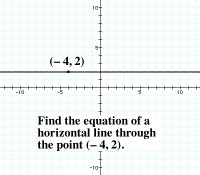
Table of Contents
How to Find the Equation of a Horizontal Line: A Comprehensive Guide
Finding the equation of a horizontal line might seem trivial at first glance, but understanding its underlying principles is crucial for grasping fundamental concepts in algebra and coordinate geometry. This comprehensive guide will delve deep into the topic, exploring various approaches, providing illustrative examples, and addressing common misconceptions. We will also examine how understanding horizontal lines can lay the groundwork for more complex mathematical concepts.
Understanding the Cartesian Coordinate System
Before we dive into finding the equation, let's refresh our understanding of the Cartesian coordinate system. This system uses two perpendicular lines, the x-axis (horizontal) and the y-axis (vertical), to define a plane. Every point on this plane can be uniquely identified by its coordinates (x, y), where 'x' represents its horizontal position and 'y' its vertical position.
Defining a Horizontal Line
A horizontal line is a straight line that runs parallel to the x-axis. This means that for every point on the line, the y-coordinate remains constant, while the x-coordinate can take any value. This constant y-value is the defining characteristic of a horizontal line.
Methods for Finding the Equation
There are several ways to determine the equation of a horizontal line, depending on the information provided.
Method 1: Using the y-intercept
The simplest method is when you know the y-intercept – the point where the line crosses the y-axis. Since the y-coordinate remains constant, the equation of a horizontal line is simply:
y = b
where 'b' is the y-intercept (the y-coordinate of any point on the line).
Example: If a horizontal line crosses the y-axis at the point (0, 3), its equation is y = 3. This means that for any x-value, the corresponding y-value will always be 3.
Method 2: Using Two Points on the Line
If you are given two points that lie on the horizontal line, you can still find the equation. Remember, the y-coordinate will be the same for both points.
Example: Let's say we have the points (2, 5) and (7, 5). Notice that the y-coordinate is 5 in both cases. Therefore, the equation of the horizontal line passing through these points is y = 5.
Method 3: Using the Slope
The slope of a horizontal line is always zero (0). The slope (m) is defined as the change in y divided by the change in x:
m = (y₂ - y₁) / (x₂ - x₁)
Since the y-coordinates are always the same on a horizontal line, the numerator (y₂ - y₁) will always be zero. This results in a slope of zero, regardless of the x-values. While you can't use the standard slope-intercept form (y = mx + b) directly because m=0, the consequence is that the equation reduces to simply y = b, as explained in Method 1.
Method 4: From a Graph
If you have a graph depicting the horizontal line, simply read the y-coordinate of any point on the line. This y-coordinate is the value of 'b' in the equation y = b.
Common Mistakes to Avoid
Several common errors can occur when finding the equation of a horizontal line:
- Confusing x and y: Remember that the equation of a horizontal line involves only the y-coordinate. Don't mistakenly use the x-coordinate.
- Incorrect Interpretation of the y-intercept: Ensure you correctly identify the y-intercept from a graph or given information.
- Using the slope-intercept form incorrectly: While you can conceptually use the slope-intercept form (y = mx + b), understanding that m = 0 simplifies the equation to y = b is crucial for efficiency and avoiding unnecessary calculations.
Applications of Horizontal Lines
Horizontal lines are fundamental in various mathematical and real-world applications:
- Graphing Functions: Horizontal lines represent constant functions, where the output (y-value) remains the same regardless of the input (x-value).
- Solving Equations: Horizontal lines can visually represent solutions to equations where 'y' is a constant.
- Geometry: Horizontal lines are used extensively in geometry, such as defining parallel lines, calculating areas, and solving geometric problems.
- Real-World Applications: Horizontal lines find applications in various fields including engineering (representing constant levels), cartography (representing lines of latitude), and data analysis (representing constant trends or averages).
Advanced Concepts and Extensions
Understanding horizontal lines forms a crucial stepping stone towards understanding more complex concepts:
- Parallel and Perpendicular Lines: Horizontal lines are parallel to each other and perpendicular to vertical lines. This forms the basis of understanding parallel and perpendicular line relationships.
- Systems of Equations: Solving systems of equations often involves identifying intersection points. When a horizontal line intersects another line, the y-coordinate of the intersection point corresponds to the y-value of the horizontal line.
- Functions and Relations: Horizontal lines are vital in determining whether a relation is a function by using the horizontal line test. If a horizontal line intersects the graph of a relation at more than one point, the relation is not a function.
- Calculus: Horizontal lines appear in calculus as tangent lines to functions at points where the derivative is zero (local maxima or minima).
Conclusion
Finding the equation of a horizontal line is a seemingly simple task, yet it underpins many essential concepts in mathematics and its applications. By understanding the fundamental principles, recognizing common mistakes, and appreciating its role in more advanced mathematical contexts, you can build a strong foundation for further learning and problem-solving in mathematics and related fields. Remember, mastering these basic concepts is key to unlocking more complex mathematical ideas. Through consistent practice and a clear understanding of the methods presented, you can confidently approach and solve problems involving horizontal lines. This understanding is not just about finding an equation; it’s about developing a deeper mathematical intuition and problem-solving capability.
Latest Posts
Latest Posts
-
Is Tap Water A Heterogeneous Mixture
Apr 07, 2025
-
How To Describe Distribution In Statistics
Apr 07, 2025
-
Identify The Functional Groups In The Following Molecules
Apr 07, 2025
-
Van Der Waals Equation A And B Values
Apr 07, 2025
-
What Are The Functions Of Language
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about How To Find Equation Of A Horizontal Line . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
