How To Find The Critical Value Of R
Muz Play
Apr 02, 2025 · 6 min read
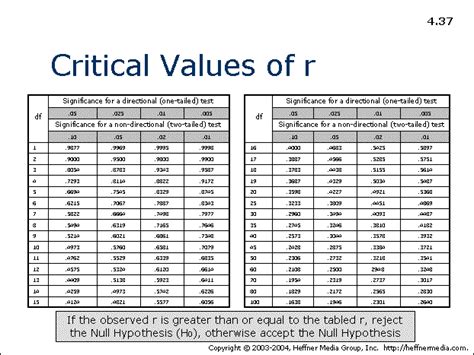
Table of Contents
How to Find the Critical Value of r: A Comprehensive Guide
Determining the critical value of the correlation coefficient, r, is crucial in hypothesis testing for correlation. It helps you decide whether the observed correlation in your sample data is strong enough to suggest a significant correlation in the population. This guide will walk you through the process, explaining the concepts and providing practical examples.
Understanding Correlation and the Correlation Coefficient (r)
Before diving into finding the critical value, let's establish a firm understanding of correlation. Correlation measures the strength and direction of a linear relationship between two variables. The correlation coefficient, r, quantifies this relationship:
- Strength: The absolute value of r indicates the strength. A value closer to 1 or -1 signifies a stronger correlation, while a value closer to 0 indicates a weaker correlation.
- Direction: The sign of r indicates the direction. A positive r implies a positive correlation (as one variable increases, the other tends to increase), while a negative r implies a negative correlation (as one variable increases, the other tends to decrease).
Example: An r value of 0.8 indicates a strong positive correlation, while an r value of -0.6 indicates a moderate negative correlation. An r value close to 0 suggests a weak or no linear relationship.
The Importance of Critical Values
In statistical hypothesis testing, we use the critical value of r to determine whether our observed correlation is statistically significant. We are essentially asking: Is the correlation we found in our sample likely to reflect a true correlation in the larger population, or is it just due to random chance?
To answer this question, we compare our calculated r value to the critical value. The critical value is the minimum value of r required to reject the null hypothesis (which states there is no correlation in the population). If our calculated r is greater than (for a positive correlation) or less than (for a negative correlation) the critical value, we reject the null hypothesis and conclude that there is a significant correlation.
Factors Affecting the Critical Value of r
Several factors influence the critical value of r:
1. Sample Size (n):
The sample size plays a significant role. Larger samples provide more reliable estimates of the population correlation. With larger samples, smaller correlations can be deemed statistically significant. Therefore, the critical value of r decreases as the sample size increases.
2. Significance Level (α):
The significance level (alpha), commonly set at 0.05 (5%), represents the probability of rejecting the null hypothesis when it is actually true (Type I error). A lower significance level (e.g., 0.01) requires a larger critical value of r, meaning a stronger correlation is needed to reject the null hypothesis.
3. One-tailed vs. Two-tailed Test:
- Two-tailed test: This tests for a correlation in either direction (positive or negative). You need to consider both positive and negative critical values.
- One-tailed test: This tests for a correlation in a specific direction (either positive or negative). You only need to consider one critical value (positive or negative, depending on your hypothesis). One-tailed tests have lower critical values than two-tailed tests for the same sample size and significance level.
How to Find the Critical Value of r: Using a Table
The most common method for finding the critical value of r is using a table of critical values for Pearson's correlation coefficient. These tables are readily available in statistics textbooks and online. They typically present critical values for different sample sizes (n) and significance levels (α).
How to Use the Table:
- Determine your sample size (n): This is the number of pairs of data points in your dataset.
- Determine your significance level (α): Commonly set at 0.05 or 0.01.
- Determine whether you are conducting a one-tailed or two-tailed test: Your hypothesis will dictate this.
- Locate the critical value: Find the intersection of your sample size and significance level in the table. The value at this intersection is your critical value.
Example:
Let's say you have a sample size of n = 20 and you are conducting a two-tailed test at a significance level of α = 0.05. Looking at a critical value table, you would find the critical value of r to be approximately 0.444. This means that if your calculated r is greater than 0.444 or less than -0.444, you can reject the null hypothesis at the 0.05 significance level.
Using Statistical Software
Statistical software packages such as SPSS, R, SAS, and Python (with libraries like SciPy) can readily calculate the critical value of r for you. These programs often provide p-values directly, eliminating the need to manually consult a table. The p-value represents the probability of observing the calculated r (or a more extreme value) if there were no correlation in the population. If the p-value is less than your significance level (α), you reject the null hypothesis.
Interpreting Results and Avoiding Common Pitfalls
-
Significance vs. Practical Significance: Just because a correlation is statistically significant doesn't automatically mean it's practically significant. A small but statistically significant correlation might not be meaningful in a real-world context. Consider the effect size and the context of your study.
-
Causation vs. Correlation: Correlation does not imply causation. Even if you find a significant correlation between two variables, it doesn't necessarily mean that one variable causes changes in the other. There could be other confounding variables involved.
-
Linearity: The correlation coefficient r measures only linear relationships. If the relationship between your variables is non-linear, r might not be an appropriate measure of association. Consider visualizing your data with a scatter plot to assess linearity before performing correlation analysis.
-
Outliers: Outliers can heavily influence the correlation coefficient. Examine your data for outliers and consider how they might be affecting your results. Robust correlation methods might be necessary if outliers are a significant concern.
Advanced Considerations
-
Spearman's Rank Correlation: If your data doesn't meet the assumptions of Pearson's correlation (e.g., normality, linearity), consider using Spearman's rank correlation, which is less sensitive to outliers and non-linearity. Critical values for Spearman's rank correlation are also available in statistical tables or software.
-
Partial Correlation: If you suspect that a third variable is confounding the relationship between your two variables of interest, consider performing a partial correlation analysis. This technique removes the influence of the third variable before calculating the correlation between the variables of interest.
-
Multiple Regression: For examining the relationship between one dependent variable and multiple independent variables, multiple regression is a more powerful technique than simple correlation.
Conclusion
Finding the critical value of r is a crucial step in hypothesis testing for correlation. Understanding the factors that influence the critical value (sample size, significance level, one-tailed vs. two-tailed test) and correctly interpreting the results are essential for drawing valid conclusions from your data. Remember that statistical significance doesn't automatically equate to practical significance, and correlation should not be misinterpreted as causation. By carefully applying the techniques described in this guide, you can confidently analyze your data and make informed inferences about the relationships between variables. Utilizing statistical software can significantly streamline the process and ensure accuracy in your analysis.
Latest Posts
Latest Posts
-
What Determines The Volume Of Gas
Apr 03, 2025
-
Non Mendelian Genetics Practice Packet Answers
Apr 03, 2025
-
Similarities Between Endocrine And Nervous System
Apr 03, 2025
-
How To Choose U And Dv In Integration By Parts
Apr 03, 2025
-
Force On A Charge Moving In A Magnetic Field
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about How To Find The Critical Value Of R . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
