How To Find The Mean For Coin Toss
Muz Play
Mar 28, 2025 · 5 min read
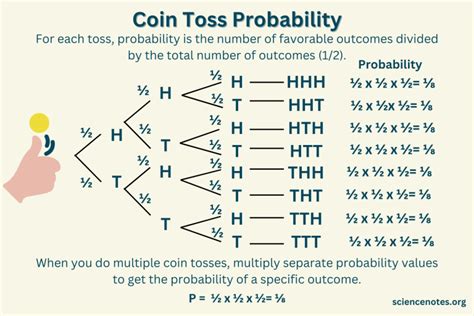
Table of Contents
How to Find the Mean for Coin Toss: A Comprehensive Guide
Flipping a coin might seem simple, but understanding its statistical properties opens doors to broader concepts in probability and statistics. This article delves deep into calculating the mean (average) result of a coin toss, exploring various scenarios, and explaining the underlying mathematical principles. We'll move beyond the simple "heads or tails" and discuss how the mean changes with different types of coins, multiple tosses, and even incorporates the fascinating world of weighted coins.
Understanding the Basics: Fair Coin Toss
A fair coin has an equal probability of landing on heads (H) or tails (T). This probability is 50%, or 0.5, for each outcome. When we talk about the mean in this context, we're interested in the average outcome over many coin tosses. Since heads and tails are typically represented by 1 and 0 respectively (or vice versa), we can easily calculate the mean.
Calculating the Mean for a Single Toss
For a single coin toss, the mean is simply the expected value. Because the probability of heads (1) is 0.5 and the probability of tails (0) is 0.5, the expected value (mean) is:
(0.5 * 1) + (0.5 * 0) = 0.5
This means that, on average, you'd expect to get 0.5 (representing a mixture of heads and tails) in a single toss. Of course, you can't actually get 0.5 in a single toss; it's a theoretical average across many tosses.
Calculating the Mean for Multiple Tosses
The mean becomes more insightful when we consider multiple coin tosses. Let's say we flip a coin 10 times. The possible outcomes range from all heads (10) to all tails (0). However, if the coin is fair, we expect an approximately equal number of heads and tails.
To calculate the mean for multiple tosses, we use the same principle of expected value. For n tosses, the expected number of heads is (n * 0.5). Therefore, the expected mean is:
(n * 0.5) / n = 0.5
The mean remains 0.5, regardless of the number of tosses. This is a crucial characteristic of the expected value – it remains consistent across numerous trials, reinforcing the concept of the law of large numbers.
Beyond the Fair Coin: Exploring Weighted Coins
The world of coin tosses isn't limited to fair coins. A weighted coin has an unequal probability of landing on heads or tails. This introduces a fascinating wrinkle to calculating the mean.
Defining the Weighted Coin
Let's consider a coin where the probability of heads is 'p' and the probability of tails is '1-p'. Notice that 'p' can be any value between 0 and 1. For example:
- p = 0.6: Heads has a 60% probability, and tails has a 40% probability.
- p = 0.2: Heads has a 20% probability, and tails has an 80% probability.
Calculating the Mean for a Weighted Coin (Single Toss)
The calculation of the mean for a single toss of a weighted coin is straightforward:
(p * 1) + ((1-p) * 0) = p
The mean is simply equal to the probability of getting heads ('p').
Calculating the Mean for a Weighted Coin (Multiple Tosses)
For multiple tosses (n) of a weighted coin, the expected number of heads is (n * p). The mean is therefore:
(n * p) / n = p
Again, the mean remains constant and equal to 'p', the probability of heads. This highlights that the mean reflects the inherent bias of the weighted coin.
Practical Applications and Real-World Examples
Understanding the mean of a coin toss isn't just a theoretical exercise. It has numerous practical applications across various fields:
1. Simulations and Modeling
Coin tosses are often used in simulations to model random events. For example, in computer simulations of complex systems, a coin toss might represent a binary decision (yes/no, success/failure). Understanding the mean helps predict the overall outcome of such simulations.
2. Game Theory and Decision Making
In game theory, coin tosses are used to determine random outcomes or to introduce an element of chance. The mean helps analyze the expected payoffs or utilities of different strategies.
3. Statistical Inference and Hypothesis Testing
Coin toss experiments form the basis of many statistical concepts, such as hypothesis testing and confidence intervals. The mean serves as a reference point for comparing observed results with expected values.
4. Monte Carlo Simulations
Monte Carlo simulations use random sampling to model complex systems. Coin tosses can be a part of such simulations, and the mean helps analyze the results and draw meaningful conclusions.
Advanced Concepts and Further Exploration
The concept of the mean in coin tosses can be expanded to more complex scenarios:
1. Sequences and Patterns
Analyzing sequences of coin tosses, such as the likelihood of consecutive heads or tails, introduces more intricate probability calculations. While the mean for individual tosses remains consistent, the probability of specific sequences changes.
2. Markov Chains
Markov chains model systems where the future state depends only on the current state. Coin tosses can be used to illustrate Markov chains, with the mean reflecting the long-term probabilities of different states.
3. Random Walks
Random walks are mathematical models where movements are random. Coin tosses can simulate a one-dimensional random walk, with the mean representing the average position after many steps.
Conclusion: The Power of the Mean in Coin Toss Analysis
Calculating the mean for a coin toss, even seemingly simple, provides a powerful foundation for understanding probability and statistical concepts. Whether dealing with fair or weighted coins, multiple tosses, or exploring more advanced scenarios, the mean serves as a crucial metric for predicting outcomes, analyzing results, and building more complex models. Mastering this fundamental concept unlocks a deeper appreciation for the mathematical underpinnings of randomness and its wide-ranging applications across various fields. By understanding the mean, we gain a clearer perspective on the unpredictable world of chance and how we can effectively analyze and interpret its results. This knowledge transcends simple coin flips and lays the groundwork for understanding more complex probabilistic events, furthering your analytical and problem-solving skills. The journey from a single coin toss to understanding the broader implications of its statistical properties is a rewarding one, offering valuable insights into the world of mathematics and beyond.
Latest Posts
Latest Posts
-
Which Of The Following Cross Couplings Of An Enolate
Mar 31, 2025
-
Primary And Secondary Growth Of Plants
Mar 31, 2025
-
Relationship Between Temperature And Kinetic Energy
Mar 31, 2025
-
10 Ejercicios De Verbos Irregulares En Ingles
Mar 31, 2025
-
What Is The Coefficient In A Chemical Equation
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about How To Find The Mean For Coin Toss . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
