Integrals Of Even And Odd Functions
Muz Play
Mar 31, 2025 · 5 min read
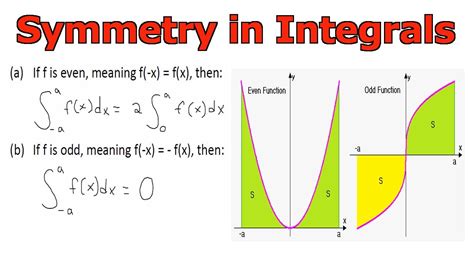
Table of Contents
Integrals of Even and Odd Functions: A Comprehensive Guide
Integrals, a cornerstone of calculus, find widespread applications across diverse fields like physics, engineering, and economics. Understanding how to evaluate integrals efficiently is crucial. This comprehensive guide delves into the fascinating world of integrals of even and odd functions, providing a solid foundation for tackling more complex integration problems. We'll explore the properties of even and odd functions, demonstrate how these properties simplify integration, and illustrate the concepts with numerous examples.
Understanding Even and Odd Functions
Before diving into integration, let's refresh our understanding of even and odd functions. A function is defined as:
-
Even Function: A function f(x) is even if f(-x) = f(x) for all x in its domain. Graphically, an even function is symmetric about the y-axis. Classic examples include f(x) = x², f(x) = cos(x), and f(x) = |x|.
-
Odd Function: A function f(x) is odd if f(-x) = -f(x) for all x in its domain. Graphically, an odd function exhibits rotational symmetry about the origin. Examples include f(x) = x, f(x) = x³, and f(x) = sin(x).
It's important to note that not all functions are either even or odd; many functions are neither.
The Power of Symmetry: Simplifying Definite Integrals
The symmetry inherent in even and odd functions significantly simplifies the evaluation of definite integrals, particularly over symmetric intervals like [-a, a]. Let's explore these simplifications:
Integrals of Even Functions
For an even function f(x), the definite integral over a symmetric interval [-a, a] can be expressed as:
∫<sub>-a</sub><sup>a</sup> f(x) dx = 2 ∫<sub>0</sub><sup>a</sup> f(x) dx
This simplification arises from the symmetry of the function. The area under the curve from -a to 0 is identical to the area from 0 to a. Therefore, we only need to calculate the integral from 0 to a and multiply by 2. This significantly reduces computational effort.
Integrals of Odd Functions
For an odd function f(x), the definite integral over a symmetric interval [-a, a] is always zero:
∫<sub>-a</sub><sup>a</sup> f(x) dx = 0
This result stems from the cancellation of areas. The area under the curve from -a to 0 is exactly the negative of the area from 0 to a. These areas cancel each other out, resulting in a net area of zero.
Practical Applications and Examples
Let's solidify our understanding with several examples:
Example 1: Even Function
Evaluate the integral: ∫<sub>-2</sub><sup>2</sup> (x² + 1) dx
Since f(x) = x² + 1 is an even function (f(-x) = (-x)² + 1 = x² + 1 = f(x)), we can use the simplification for even functions:
∫<sub>-2</sub><sup>2</sup> (x² + 1) dx = 2 ∫<sub>0</sub><sup>2</sup> (x² + 1) dx = 2 [(x³/3 + x) ]<sub>0</sub><sup>2</sup> = 2 [(8/3 + 2) - 0] = 2 (14/3) = 28/3
Example 2: Odd Function
Evaluate the integral: ∫<sub>-π</sub><sup>π</sup> sin(x) dx
Since f(x) = sin(x) is an odd function (f(-x) = sin(-x) = -sin(x) = -f(x)), the integral over the symmetric interval [-π, π] is:
∫<sub>-π</sub><sup>π</sup> sin(x) dx = 0
Example 3: A Function that is Neither Even Nor Odd
Evaluate the integral: ∫<sub>-1</sub><sup>1</sup> (x³ + x²) dx
The function f(x) = x³ + x² is neither even nor odd. We cannot use the simplifications for even or odd functions. We must evaluate the integral directly:
∫<sub>-1</sub><sup>1</sup> (x³ + x²) dx = [(x⁴/4) + (x³/3)]<sub>-1</sub><sup>1</sup> = [(1/4 + 1/3) - (1/4 - 1/3)] = 2/3
Example 4: Piecewise Defined Function
Consider the integral of a piecewise function:
f(x) = { x², x ≥ 0; -x², x < 0}
This function is an even function because f(-x) = -(-x)² = -x² = f(x). Therefore the integral from -a to a can be simplified.
Example 5: Involving Trigonometric Functions
Evaluate ∫<sub>-π/2</sub><sup>π/2</sup> cos(x) dx
Cosine is an even function, therefore:
∫<sub>-π/2</sub><sup>π/2</sup> cos(x) dx = 2 ∫<sub>0</sub><sup>π/2</sup> cos(x) dx = 2 [sin(x)]<sub>0</sub><sup>π/2</sup> = 2 (1 - 0) = 2
Advanced Applications and Extensions
The concepts of even and odd functions extend beyond basic integration. They prove invaluable in:
-
Fourier Series: Even and odd functions play a fundamental role in representing periodic functions using Fourier series. The coefficients of the series are simplified significantly when dealing with even or odd functions.
-
Probability and Statistics: In probability theory, certain probability density functions exhibit even or odd symmetry, leading to simplifications in calculating moments and other statistical properties.
-
Partial Differential Equations: Solving partial differential equations often involves utilizing the properties of even and odd functions to simplify the solution process, particularly in problems with symmetry.
Conclusion: Mastering Integrals of Even and Odd Functions
Understanding and applying the properties of even and odd functions dramatically streamlines the process of evaluating definite integrals. By recognizing the symmetry inherent in these functions, we can significantly reduce computational complexity and gain valuable insights into the problem at hand. This knowledge is not only essential for mastering calculus but also extends to various advanced applications across numerous scientific and engineering disciplines. Proficiency in this area will undoubtedly enhance your problem-solving capabilities and deepen your understanding of mathematical principles. Remember to always check if the integrand is even or odd, especially when dealing with symmetric intervals. This simple check can save you considerable time and effort.
Latest Posts
Latest Posts
-
Is As A Metal Nonmetal Or Metalloid
Apr 02, 2025
-
The Process Of Getting Information Into Memory Is Called
Apr 02, 2025
-
Where Are Nonmetals Located In The Periodic Table
Apr 02, 2025
-
Write An Equation Any Form For The Quadratic Graphed Below
Apr 02, 2025
-
What Is The Chromosomal Basis Of Inheritance
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Integrals Of Even And Odd Functions . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
