Is Kinetic Energy Conserved In An Elastic Collision
Muz Play
Mar 26, 2025 · 6 min read
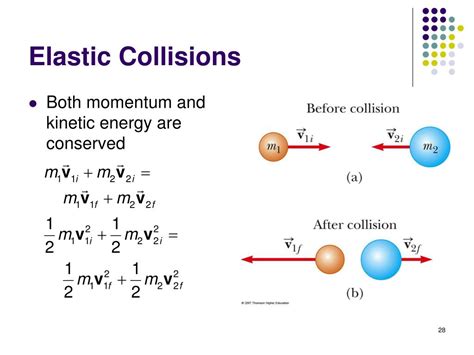
Table of Contents
Is Kinetic Energy Conserved in an Elastic Collision? A Deep Dive
The principle of conservation of energy is a cornerstone of physics, stating that energy cannot be created or destroyed, only transformed from one form to another. A crucial aspect of this principle involves understanding how kinetic energy, the energy of motion, behaves in different types of collisions. This article will explore the question: Is kinetic energy conserved in an elastic collision? We'll delve into the definition of elastic collisions, examine the theoretical underpinnings of kinetic energy conservation in such events, and explore real-world examples and scenarios where this principle plays a crucial role.
Understanding Elastic Collisions
Before investigating kinetic energy conservation, it's essential to define what constitutes an elastic collision. In an elastic collision, both momentum and kinetic energy are conserved. This means the total kinetic energy of the system before the collision is equal to the total kinetic energy after the collision. No energy is lost to other forms, such as heat, sound, or deformation. This is an idealized scenario; perfectly elastic collisions rarely occur in the real world. However, some collisions approximate elastic behavior closely enough to be considered practically elastic for many purposes.
Key Characteristics of Elastic Collisions:
- Conservation of Kinetic Energy: This is the defining characteristic. The sum of the kinetic energies of all objects involved remains constant throughout the collision.
- Conservation of Momentum: The total momentum of the system (the vector sum of the individual momenta) is also conserved. This means the total momentum before the collision equals the total momentum after the collision.
- No Energy Loss: No energy is transformed into other forms, such as heat, sound, or deformation. The colliding objects rebound with the same total kinetic energy they possessed initially.
- Idealized Model: While perfectly elastic collisions are rare, many collisions can be modeled as elastic for simplification and accuracy within a certain tolerance.
The Physics Behind Kinetic Energy Conservation in Elastic Collisions
The conservation of kinetic energy in elastic collisions is a direct consequence of Newton's laws of motion and the assumption of perfectly elastic interaction between the colliding objects. Let's examine this in detail:
Newton's Laws and the Conservation of Momentum:
Newton's third law states that for every action, there is an equal and opposite reaction. In a collision, this translates to the forces exerted between the colliding objects being equal in magnitude and opposite in direction. This equality of forces, acting over the same time interval, leads to the conservation of momentum.
The Role of Elasticity:
Elasticity refers to the ability of an object to return to its original shape and size after being deformed by a force. In a perfectly elastic collision, the objects deform momentarily during contact, but the deformation is entirely reversed, and no energy is lost to permanent deformation. This ensures that the kinetic energy is not converted into other forms of energy.
Mathematical Representation of Kinetic Energy Conservation
Let's consider a simple case of two objects, object A and object B, with masses m<sub>A</sub> and m<sub>B</sub>, and initial velocities u<sub>A</sub> and u<sub>B</sub>, respectively. After the elastic collision, their velocities are v<sub>A</sub> and v<sub>B</sub>.
The conservation of kinetic energy can be expressed mathematically as:
(1/2)m<sub>A</sub>u<sub>A</sub>² + (1/2)m<sub>B</sub>u<sub>B</sub>² = (1/2)m<sub>A</sub>v<sub>A</sub>² + (1/2)m<sub>B</sub>v<sub>B</sub>²
This equation states that the total kinetic energy before the collision (left side) is equal to the total kinetic energy after the collision (right side).
Similarly, the conservation of momentum is represented by:
m<sub>A</sub>u<sub>A</sub> + m<sub>B</sub>u<sub>B</sub> = m<sub>A</sub>v<sub>A</sub> + m<sub>B</sub>v<sub>B</sub>
These two equations, used simultaneously, allow us to solve for the final velocities (v<sub>A</sub> and v<sub>B</sub>) if the initial velocities and masses are known.
Examples of (Near-)Elastic Collisions
While perfectly elastic collisions are rare, many real-world events approximate elastic behavior sufficiently for practical purposes:
- Collision of Billiard Balls: The collision between billiard balls is a commonly cited example. While some energy is lost as sound and perhaps slight deformation, the loss is relatively small, and the collision is often treated as elastic in simplified calculations.
- Collision of Atoms or Subatomic Particles: At the atomic and subatomic level, collisions often exhibit near-elastic behavior. The interactions are governed by fundamental forces, and energy loss due to other processes is minimal.
- Superballs: These toys are designed to exhibit high elasticity, bouncing back to a significant percentage of their initial height. While not perfectly elastic, they provide a good demonstration of near-elastic behavior.
- Collisions of perfectly rigid bodies in an ideal environment: Though hypothetical in reality, this scenario perfectly illustrates the principle of conservation of kinetic energy during elastic collision.
Inelastic Collisions: A Contrast
To further understand elastic collisions, it's helpful to compare them with inelastic collisions. In an inelastic collision, kinetic energy is not conserved. Some kinetic energy is transformed into other forms of energy, such as heat, sound, or deformation. The total energy of the system is still conserved (according to the law of conservation of energy), but the kinetic energy is reduced.
Characteristics of Inelastic Collisions:
- Kinetic Energy is Not Conserved: The total kinetic energy after the collision is less than the total kinetic energy before the collision.
- Momentum is Conserved: Despite the loss of kinetic energy, the total momentum of the system is still conserved.
- Energy Transformation: The lost kinetic energy is converted into other forms of energy, such as heat, sound, or the energy of permanent deformation.
- Examples: Most everyday collisions are inelastic, including car crashes, balls of clay colliding, or a ball hitting the ground.
Real-World Implications and Applications
Understanding elastic and inelastic collisions is crucial in many fields:
- Engineering: Designing structures and systems that can withstand impacts requires considering the energy transfer during collisions. For example, designing safety features in vehicles involves understanding inelastic collisions to mitigate injuries.
- Physics: Elastic collisions are crucial in understanding the behavior of particles in various systems, from atoms to galaxies. This understanding helps in modeling and predicting the behavior of these systems.
- Sports: The principles of elastic and inelastic collisions are important in analyzing the dynamics of many sports, such as tennis, golf, and baseball. The bounce of a ball, the impact of a racket on a ball – these are all examples of collisions with varying degrees of elasticity.
Conclusion: A Fundamental Principle
The conservation of kinetic energy in elastic collisions is a fundamental principle in physics with far-reaching implications. While perfectly elastic collisions are an idealization, understanding this principle allows us to model and analyze a wide range of real-world phenomena, from the impact of a tennis ball to the behavior of subatomic particles. By contrasting elastic collisions with inelastic ones, we gain a deeper understanding of energy transformations and their importance in various scientific and engineering applications. The equations presented serve as a solid mathematical foundation for further exploration and application of these concepts. Remember that while the theoretical ideal is important, the practical application often necessitates approximations, acknowledging the real-world complexities that lead to deviations from perfect elasticity.
Latest Posts
Latest Posts
-
Use The Cofactor Expansion To Compute The Following Determinant
Mar 29, 2025
-
How To Find Point Of Tangency
Mar 29, 2025
-
How Do You Calculate Potential Difference
Mar 29, 2025
-
How To Round To Four Decimal Places
Mar 29, 2025
-
Reaction Of Benzoic Acid And Naoh
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Is Kinetic Energy Conserved In An Elastic Collision . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
