Loop Of Wire In A Magnetic Field
Muz Play
Mar 28, 2025 · 5 min read
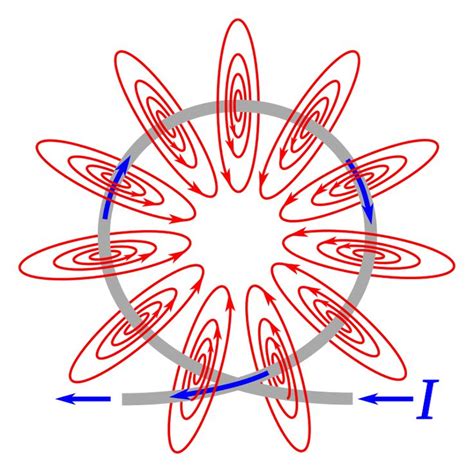
Table of Contents
Loop of Wire in a Magnetic Field: A Comprehensive Guide
A loop of wire placed within a magnetic field provides a fascinating demonstration of the interplay between electricity and magnetism, forming the basis of numerous technologies we use daily. Understanding how a loop of wire behaves in a magnetic field is crucial for grasping concepts in electromagnetism, from electric generators and motors to transformers and inductors. This comprehensive guide explores the fundamental principles, equations, and applications surrounding this intriguing phenomenon.
Understanding the Fundamentals: Magnetic Flux and Faraday's Law
Before diving into the specifics of a loop of wire in a magnetic field, let's establish some fundamental concepts. The key to understanding the behavior of the loop lies in magnetic flux. Magnetic flux (Φ) is a measure of the total magnetic field that passes through a given area. It's calculated as:
Φ = B * A * cos(θ)
Where:
- B represents the magnetic field strength (Tesla).
- A represents the area of the loop (square meters).
- θ represents the angle between the magnetic field lines and the normal to the plane of the loop.
The significance of magnetic flux becomes apparent when considering Faraday's Law of Electromagnetic Induction. This law states that a changing magnetic flux through a loop of wire induces an electromotive force (EMF), or voltage, in the loop. Mathematically:
EMF = -dΦ/dt
This equation reveals that the induced EMF is directly proportional to the rate of change of magnetic flux. The negative sign signifies Lenz's Law, which dictates that the induced current will flow in a direction that opposes the change in magnetic flux.
Exploring Different Scenarios: Static vs. Changing Magnetic Fields
The behavior of a loop of wire in a magnetic field significantly differs depending on whether the magnetic field is static or changing.
1. Static Magnetic Field: No Induced Current
If a loop of wire is placed in a uniform, static magnetic field, meaning the magnetic field strength and direction remain constant, no EMF is induced. This is because the magnetic flux through the loop remains constant (dΦ/dt = 0), resulting in zero induced EMF according to Faraday's Law. While there's no induced current, the loop will still experience a magnetic force if it carries a current.
2. Changing Magnetic Field: Induced Current and EMF
The scenario becomes considerably more interesting when the magnetic field is changing. Several ways to achieve this change include:
-
Moving the loop: Moving the loop in a static magnetic field alters the magnetic flux through the loop as the area of the loop intersecting the field lines changes. This change in flux induces an EMF.
-
Changing the magnetic field strength: Increasing or decreasing the strength of the magnetic field passing through a stationary loop will also change the magnetic flux, inducing an EMF.
-
Rotating the loop: Rotating a loop within a static magnetic field changes the angle (θ) between the magnetic field lines and the loop's normal, resulting in a change in magnetic flux and thus an induced EMF. This principle is fundamental to the operation of electric generators.
The magnitude and direction of the induced current depend on the rate of change of the magnetic flux and the resistance of the wire. A faster change in flux leads to a larger induced EMF and current.
Applications: From Generators to Transformers
The principle of a loop of wire in a changing magnetic field underpins numerous crucial applications in electrical engineering and technology:
1. Electric Generators: Harnessing Mechanical Energy
Electric generators utilize the principle of electromagnetic induction to convert mechanical energy into electrical energy. They typically consist of a loop of wire rotating within a strong magnetic field. The rotation continuously changes the magnetic flux through the loop, inducing an alternating current (AC). The frequency of the AC depends on the rotation speed of the loop.
2. Electric Motors: Converting Electrical Energy into Mechanical Energy
Electric motors work on a reciprocal principle to generators. They use an electric current flowing through a loop of wire placed in a magnetic field to generate a magnetic force, causing the loop to rotate. This rotational motion can then be used to perform mechanical work.
3. Transformers: Efficient Energy Transfer
Transformers rely on electromagnetic induction to change the voltage of an alternating current. They consist of two coils of wire, a primary and a secondary coil, wrapped around a common ferromagnetic core. An alternating current in the primary coil creates a changing magnetic field which, in turn, induces an alternating current in the secondary coil. The voltage ratio between the primary and secondary coils is determined by the ratio of the number of turns in each coil.
4. Induction Cooktops: Efficient Heating
Induction cooktops use a changing magnetic field to induce eddy currents within the ferromagnetic base of a cooking pot. These eddy currents generate heat, efficiently cooking the food.
Advanced Concepts and Considerations
The simple model of a single loop of wire in a magnetic field provides a solid foundation, but several complexities emerge when dealing with real-world applications:
-
Self-Inductance: A changing current in a loop of wire itself creates a changing magnetic field that induces a back EMF in the same loop. This phenomenon is known as self-inductance and is crucial in understanding the behavior of inductors.
-
Mutual Inductance: Two or more loops of wire in close proximity can influence each other's magnetic fields. A changing current in one loop induces an EMF in the other, a concept known as mutual inductance, critical for transformers and other coupled circuits.
-
Non-uniform Magnetic Fields: Many real-world applications involve non-uniform magnetic fields, requiring more complex mathematical treatments to accurately predict the induced EMF.
-
Eddy Currents: In conductive materials placed within a changing magnetic field, circulating currents, known as eddy currents, are induced. These currents can cause energy loss in some applications but are exploited in others, such as induction braking and induction heating.
Conclusion: A Fundamental Concept with Broad Applications
The simple concept of a loop of wire in a magnetic field serves as a cornerstone of electromagnetic theory and its diverse applications. From generating electricity to precisely controlling motors and facilitating efficient energy transfer, the principles discussed here underpin many technologies that shape modern society. Understanding the interplay between magnetic flux, Faraday's Law, and Lenz's Law provides invaluable insights into the behavior of electrical circuits and electromechanical systems. As technology continues to evolve, this fundamental principle will remain central to advancements in various fields, emphasizing its enduring importance in the realm of physics and engineering.
Latest Posts
Latest Posts
-
What Are The Three General Characteristics Of Connective Tissue
Mar 31, 2025
-
Blocks Myosin Binding Sites On Actin
Mar 31, 2025
-
Label The Microscopic Structure Of A Skeletal Muscle
Mar 31, 2025
-
What Is The Difference Between Intermolecular Forces And Intramolecular Forces
Mar 31, 2025
-
Sampling With Replacement And Sampling Without Replacement
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Loop Of Wire In A Magnetic Field . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
