Magnetic Field Between Two Parallel Wires
Muz Play
Apr 05, 2025 · 6 min read
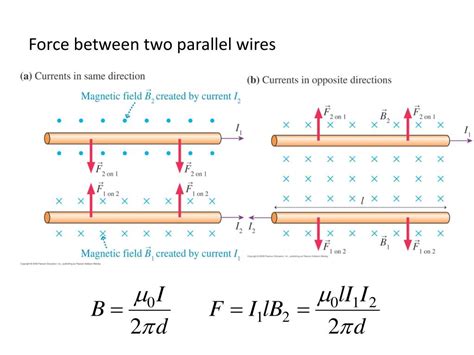
Table of Contents
Magnetic Field Between Two Parallel Wires: A Deep Dive
The magnetic field generated by current-carrying conductors is a fundamental concept in electromagnetism with wide-ranging applications. Understanding this field, particularly the interaction between parallel wires, is crucial in various fields, from designing electrical circuits to understanding the principles behind powerful electromagnets. This comprehensive article delves into the magnetic field between two parallel wires, exploring its characteristics, calculation, and practical implications.
Understanding the Magnetic Field Around a Single Wire
Before examining the interaction between two wires, let's establish a solid foundation by understanding the magnetic field produced by a single, infinitely long, straight wire carrying a current. This is best described using Ampere's Law, which relates the magnetic field around a closed loop to the current passing through the loop.
Ampere's Law and its Application
Ampere's Law states that the line integral of the magnetic field B around a closed loop is equal to the permeability of free space (μ₀) times the current (I) enclosed by the loop. Mathematically:
∮ B ⋅ dl = μ₀I
For a long straight wire, we choose a circular Amperian loop concentric with the wire. Due to symmetry, the magnetic field is constant in magnitude and tangential to the loop at every point. This simplifies the integral significantly, leading to the following expression for the magnetic field at a distance 'r' from the wire:
B = (μ₀I)/(2πr)
This equation reveals that the magnetic field strength is directly proportional to the current and inversely proportional to the distance from the wire. The direction of the magnetic field is determined by the right-hand rule: if you curl your right-hand fingers in the direction of the current, your thumb points in the direction of the magnetic field.
The Interaction of Magnetic Fields: Two Parallel Wires
Now, let's consider two infinitely long, parallel wires separated by a distance 'd', each carrying currents I₁ and I₂. The magnetic field at any point in space is the vector sum of the individual magnetic fields produced by each wire.
Superposition Principle
The superposition principle dictates that the total magnetic field at any point is the vector sum of the magnetic fields produced by each individual current source. This principle simplifies the calculation of the net magnetic field between the two wires.
Calculating the Magnetic Field Between the Wires
Let's calculate the magnetic field at a point 'P' located between the two wires, at a distance 'x' from the first wire (carrying current I₁).
- Field due to wire 1: B₁ = (μ₀I₁)/(2πx)
- Field due to wire 2: B₂ = (μ₀I₂)/(2π(d-x))
The direction of B₁ and B₂ depends on the direction of the currents. If the currents are in the same direction (parallel), the magnetic fields between the wires will be in opposite directions. If the currents are in opposite directions (anti-parallel), the magnetic fields will add up.
For parallel currents (I₁ and I₂ in the same direction): The net magnetic field at point P is the difference between the fields from each wire:
B_net = B₁ - B₂ = (μ₀I₁)/(2πx) - (μ₀I₂)/(2π(d-x))
For anti-parallel currents (I₁ and I₂ in opposite directions): The net magnetic field at point P is the sum of the fields from each wire:
B_net = B₁ + B₂ = (μ₀I₁)/(2πx) + (μ₀I₂)/(2π(d-x))
Force Between Parallel Wires
The interaction between the magnetic fields of the two wires results in a force between them. This force is given by:
F = (μ₀I₁I₂l)/(2πd)
where 'l' is the length of the wires. This equation shows that the force is directly proportional to the product of the currents and the length of the wires, and inversely proportional to the distance between them.
If the currents are in the same direction, the force is attractive, pulling the wires together. If the currents are in opposite directions, the force is repulsive, pushing the wires apart. This is a crucial concept in understanding the design of electrical circuits and the behavior of current-carrying conductors.
Practical Applications and Implications
The principles discussed above have far-reaching applications across various domains.
Electrical Circuit Design
Understanding the magnetic forces between parallel wires is essential for designing and optimizing electrical circuits. Engineers need to account for these forces to prevent damage or unintended interactions between conductors. Proper spacing and insulation are critical to minimize these effects.
Electromagnets
Electromagnets rely on the magnetic field produced by current-carrying coils of wire. By understanding the magnetic field between parallel wires, engineers can design powerful and efficient electromagnets for applications such as motors, generators, and magnetic resonance imaging (MRI) machines. The arrangement and spacing of the coils significantly influence the strength and uniformity of the magnetic field produced.
Transmission Lines
High-voltage power transmission lines use parallel wires to carry large currents over long distances. The forces between these wires are substantial, and engineers must design robust support structures to withstand these forces and prevent sagging or damage. The spacing between the wires is carefully chosen to balance the need for minimizing the magnetic field and maintaining structural integrity.
Magnetic Levitation (Maglev) Trains
Maglev trains utilize the repulsive forces between parallel conductors to achieve levitation. Electromagnets on the train and on the track interact to create a repulsive force that lifts the train above the track, reducing friction and enabling high speeds. The precise control of the magnetic fields is vital for the safety and operation of these trains.
Advanced Considerations
The analysis presented above assumes infinitely long, straight wires. In reality, wires have finite lengths and may be curved. These factors introduce complexities in calculating the magnetic field. For such scenarios, more sophisticated techniques like the Biot-Savart Law are necessary.
Biot-Savart Law
The Biot-Savart Law provides a more general approach to calculating the magnetic field produced by a current-carrying conductor of arbitrary shape. It expresses the contribution to the magnetic field at a given point due to a small segment of the conductor. Integrating over the entire conductor allows for determining the total magnetic field. This law is particularly useful for calculating the magnetic field due to wire segments of finite length or wires with complex geometries.
Skin Effect
At high frequencies, the current tends to concentrate near the surface of a conductor, a phenomenon known as the skin effect. This effect alters the distribution of the current within the wire, which, in turn, modifies the magnetic field distribution. It's essential to consider the skin effect when dealing with high-frequency applications.
Proximity Effect
The proximity effect refers to the redistribution of current within conductors due to the presence of nearby conductors. This effect becomes significant when conductors are close together and carrying large currents. It can affect the impedance and power losses in the conductors.
Conclusion
The magnetic field between two parallel wires is a fundamental concept in electromagnetism with far-reaching consequences. Understanding the principles governing this field is essential for various engineering applications, from circuit design to the development of sophisticated technologies such as maglev trains. While the analysis for infinitely long, straight wires provides a useful foundation, more advanced techniques such as the Biot-Savart Law are necessary for more complex scenarios, requiring consideration of factors like finite wire length, the skin effect, and the proximity effect. A thorough understanding of these concepts enables engineers and scientists to design and optimize electrical systems, ensuring safety, efficiency, and optimal performance. The interaction between parallel wires exemplifies the power and elegance of electromagnetic principles and their pervasive influence on modern technology.
Latest Posts
Latest Posts
-
Who Are The Different Users Of Accounting Information
Apr 06, 2025
-
Which Of The Following Are Chemical Properties Of Matter
Apr 06, 2025
-
How Do Intermolecular Forces Affect The Shape Of A Drop
Apr 06, 2025
-
Does A Prokaryotic Cell Have Ribosomes
Apr 06, 2025
-
What Is The Correct Order Of Events For Cellular Respiration
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Magnetic Field Between Two Parallel Wires . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
