Moment Of Inertia Of A Circle Formula
Muz Play
Mar 31, 2025 · 6 min read
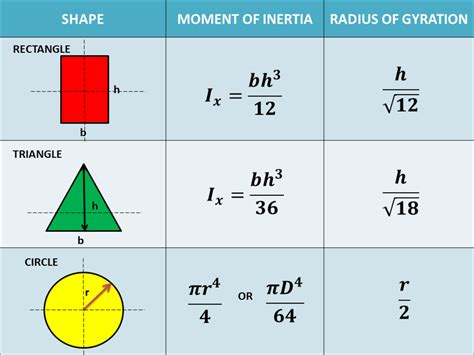
Table of Contents
Moment of Inertia of a Circle: A Comprehensive Guide
The moment of inertia, a crucial concept in physics and engineering, quantifies an object's resistance to changes in its rotation. Understanding the moment of inertia is fundamental to analyzing rotational motion, from the spin of a flywheel to the orbit of a planet. This article delves deep into the moment of inertia of a circle, exploring its derivation, applications, and variations depending on the axis of rotation. We’ll cover both solid and hollow circles, providing you with a comprehensive understanding of this important concept.
What is Moment of Inertia?
Before diving into the specifics of circular objects, let's establish a firm grasp of the fundamental concept of moment of inertia. It's essentially a rotational analog of mass in linear motion. While mass resists changes in linear velocity, the moment of inertia resists changes in angular velocity. The greater the moment of inertia, the harder it is to start or stop an object's rotation, or to change its rotational speed.
Mathematically, the moment of inertia (I) for a point mass (m) at a distance (r) from the axis of rotation is defined as:
I = mr²
For extended objects like circles, we need to integrate the contributions of all the infinitesimal mass elements that constitute the object. This integration process accounts for the varying distances of these elements from the axis of rotation. The general formula for the moment of inertia of a continuous mass distribution is:
I = ∫r² dm
Where:
- I represents the moment of inertia.
- r is the perpendicular distance of the infinitesimal mass element (dm) from the axis of rotation.
- dm represents an infinitesimal mass element within the object.
- ∫ denotes integration over the entire mass distribution of the object.
This integration can be quite complex depending on the object's shape and the chosen axis of rotation. Fortunately, for common shapes like circles, the integrals have been solved and readily available formulas exist.
Moment of Inertia of a Solid Disc (or Cylinder)
A solid disc or cylinder is a uniformly dense circular object with a finite thickness. Let's derive the moment of inertia for such an object when the axis of rotation passes through its center and is perpendicular to its plane.
We can treat the disc as a collection of concentric rings. Consider a thin ring of radius 'r' and thickness 'dr'. The area of this ring is approximately 2πr dr. If the disc has a mass per unit area (surface density) σ, the mass of this ring (dm) is:
dm = σ (2πr dr)
Substituting this into the general moment of inertia formula:
I = ∫r² dm = ∫r² σ (2πr dr)
The integration limits are from r = 0 to r = R, where R is the radius of the disc. The surface density σ can be expressed as M/(πR²), where M is the total mass of the disc. Substituting and simplifying, we get:
I = (2πσ/R²) ∫₀ᴿ r³ dr = (2πσ/R²) [r⁴/4]₀ᴿ = (2πσ/R²) (R⁴/4) = (1/2)MR²
Therefore, the moment of inertia of a solid disc or cylinder about an axis through its center and perpendicular to its plane is:
I = (1/2)MR²
This is a fundamental formula frequently used in various physics and engineering applications.
Moment of Inertia of a Thin Circular Hoop (or Ring)
A thin circular hoop or ring has all its mass concentrated at a single radius. This simplifies the calculation significantly. Consider a hoop of mass M and radius R. Since all the mass is at a distance R from the axis of rotation (through the center and perpendicular to the plane), the moment of inertia is simply:
I = MR²
This is because the integration becomes trivial: every infinitesimal mass element is at the same distance R from the axis. Note that the moment of inertia of a hoop is twice that of a solid disc of the same mass and radius. This reflects the fact that the mass is distributed further from the axis in the hoop.
Moment of Inertia of a Hollow Cylinder
A hollow cylinder, also known as a cylindrical shell, is similar to a hoop but with a finite thickness. Deriving the moment of inertia requires a slightly more involved integration process. It involves considering the cylindrical shell as a collection of concentric rings and integrating over the radial thickness. The final result, however, is:
I = ½M(R₁² + R₂²)
Where:
- M is the total mass of the hollow cylinder.
- R₁ is the inner radius of the cylinder.
- R₂ is the outer radius of the cylinder.
If the thickness of the shell is negligible compared to the radius (i.e., R₂ ≈ R₁ = R), the formula simplifies to the moment of inertia of a thin hoop: I = MR²
Moment of Inertia of a Circle about a Diameter
The moment of inertia of a circular object can vary depending on the axis of rotation. We've considered axes through the center and perpendicular to the plane. Let's now examine the scenario where the axis of rotation is a diameter of the circle.
For a solid disc, the moment of inertia about a diameter is:
I = (1/4)MR²
This is half the value obtained when the axis passes through the center and is perpendicular to the plane. This difference arises because the mass distribution is differently positioned relative to the axis of rotation. The derivation of this formula involves a more complex double integral, often using polar coordinates.
For a thin hoop about a diameter, the moment of inertia is:
I = (1/2)MR²
Again, this is half the value when the axis passes through the center and is perpendicular to the plane.
Parallel Axis Theorem
The Parallel Axis Theorem is a powerful tool for calculating the moment of inertia of an object about an axis parallel to an axis through its center of mass. It states that:
I = I<sub>cm</sub> + Md²
Where:
- I is the moment of inertia about the parallel axis.
- I<sub>cm</sub> is the moment of inertia about the axis through the center of mass.
- M is the total mass of the object.
- d is the perpendicular distance between the two parallel axes.
This theorem significantly simplifies calculations, allowing you to determine the moment of inertia about any axis parallel to one already known. For instance, if you know the moment of inertia of a disc about its center, you can easily calculate its moment of inertia about any other axis parallel to this central axis.
Applications of Moment of Inertia of a Circle
The moment of inertia of a circle, in its various forms, finds wide-ranging applications in diverse fields:
- Rotational Dynamics: Calculating angular acceleration, torque, and angular momentum of rotating circular objects like wheels, gears, and flywheels.
- Mechanical Engineering: Designing rotating machinery, analyzing stress and strain on rotating components, and optimizing energy efficiency.
- Aerospace Engineering: Analyzing the stability and control of spinning satellites and aircraft components.
- Civil Engineering: Calculating the torsional stiffness of circular columns and shafts.
- Physics: Studying the motion of planets, gyroscopes, and other rotating systems.
Conclusion
Understanding the moment of inertia of a circle is paramount for anyone working with rotational motion. The different formulas derived in this article, coupled with the Parallel Axis Theorem, provide a comprehensive toolkit for tackling various problems related to rotational dynamics. Remember to carefully consider the axis of rotation and the shape of the circular object (solid, hollow, thin hoop) to select the appropriate formula. This knowledge empowers you to analyze, design, and optimize systems involving rotational motion across diverse engineering and scientific disciplines. By grasping these concepts, you can effectively contribute to advancements in various fields.
Latest Posts
Latest Posts
-
The Process Of Getting Information Into Memory Is Called
Apr 02, 2025
-
Where Are Nonmetals Located In The Periodic Table
Apr 02, 2025
-
Write An Equation Any Form For The Quadratic Graphed Below
Apr 02, 2025
-
What Is The Chromosomal Basis Of Inheritance
Apr 02, 2025
-
Two Different Ionic Compounds Each Contain
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Moment Of Inertia Of A Circle Formula . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
