Newton's Second Law For Rotational Motion
Muz Play
Mar 29, 2025 · 6 min read
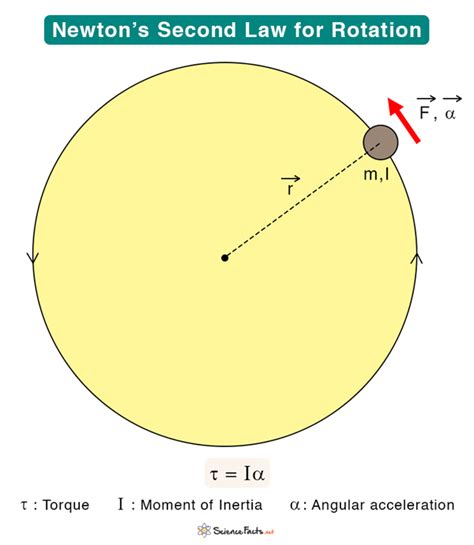
Table of Contents
Newton's Second Law for Rotational Motion: A Deep Dive
Newton's laws of motion are fundamental to classical mechanics, providing a framework for understanding how objects move under the influence of forces. While Newton's first and third laws have straightforward rotational counterparts, Newton's second law requires a more nuanced understanding when applied to rotating bodies. This article delves into the intricacies of Newton's second law for rotational motion, exploring its formulation, applications, and significance in various fields.
Understanding Linear and Rotational Motion
Before diving into the specifics of rotational motion, let's establish a clear understanding of the relationship between linear and rotational quantities. In linear motion, we deal with concepts like displacement, velocity, and acceleration, all described by vectors that point in a specific direction. Force, as described by Newton's second law (F=ma), directly causes a change in linear momentum.
Rotational motion, however, involves the rotation of an object around an axis. Instead of linear displacement, we use angular displacement (θ), measured in radians. Similarly, angular velocity (ω) represents the rate of change of angular displacement, and angular acceleration (α) represents the rate of change of angular velocity. These angular quantities are analogous to their linear counterparts but describe rotational motion.
Key Analogies Between Linear and Rotational Motion
| Linear Quantity | Rotational Quantity | Unit |
|---|---|---|
| Displacement (x) | Angular Displacement (θ) | Radians (rad) |
| Velocity (v) | Angular Velocity (ω) | Radians/second (rad/s) |
| Acceleration (a) | Angular Acceleration (α) | Radians/second² (rad/s²) |
| Mass (m) | Moment of Inertia (I) | Kilogram-meter² (kg·m²) |
| Force (F) | Torque (τ) | Newton-meter (N·m) |
| Linear Momentum (p=mv) | Angular Momentum (L=Iω) | kg·m²/s |
Newton's Second Law for Rotation: Torque and Angular Acceleration
Newton's second law for linear motion states that the net force acting on an object is equal to the product of its mass and acceleration: F = ma. The rotational equivalent of this law focuses on torque (τ) and angular acceleration (α).
Torque, the rotational analogue of force, is the tendency of a force to cause rotation around an axis. It's calculated as the product of the force and the perpendicular distance from the axis of rotation to the line of action of the force: τ = rFsinθ, where 'r' is the distance, 'F' is the force, and 'θ' is the angle between the force vector and the lever arm (the distance vector).
Moment of inertia (I) is the rotational equivalent of mass. It represents an object's resistance to changes in its rotational motion. It depends on the object's mass distribution and the axis of rotation. For a point mass, I = mr², but for more complex shapes, the calculation becomes significantly more involved, often requiring integration techniques.
Therefore, Newton's second law for rotational motion states:
τ = Iα
This equation indicates that the net torque acting on a rigid body is equal to the product of its moment of inertia and its angular acceleration. A larger torque leads to a greater angular acceleration, and a larger moment of inertia implies a greater resistance to angular acceleration.
Applications of Newton's Second Law for Rotational Motion
Newton's second law for rotational motion finds extensive application in various fields, including:
1. Engineering: Designing Rotating Machinery
Engineers utilize this law extensively in the design and analysis of rotating machinery such as turbines, motors, and flywheels. Understanding the relationship between torque, moment of inertia, and angular acceleration is crucial for determining the power requirements, structural integrity, and efficiency of these systems. For instance, designing a flywheel with a specific moment of inertia allows engineers to control its rotational energy storage capacity.
2. Physics: Analyzing Rotational Dynamics
In physics, this law is fundamental to understanding the dynamics of rotating systems. From analyzing the motion of planets around the sun to investigating the spinning of molecules, Newton's second law for rotation is indispensable. For example, it helps in calculating the angular acceleration of a spinning top or the precession of a gyroscope.
3. Sports Science: Improving Athletic Performance
In sports, understanding rotational motion is vital for optimizing athletic performance. Analyzing the angular momentum of a baseball bat during a swing, or the rotational motion of a diver during a somersault, helps identify techniques to maximize speed and efficiency. Coaches and athletes can use this knowledge to improve training methods and enhance athletic performance.
Moment of Inertia: A Closer Look
The moment of inertia (I) plays a crucial role in Newton's second law for rotational motion. Its value depends not only on the mass of the object but also on how that mass is distributed relative to the axis of rotation. Objects with mass concentrated further from the axis of rotation have a larger moment of inertia than those with mass concentrated closer to the axis.
Calculating the moment of inertia for simple shapes like rods, disks, and spheres is relatively straightforward using standard formulas. However, for more complex shapes, integration techniques are often necessary. The parallel axis theorem and the perpendicular axis theorem are valuable tools for simplifying such calculations.
Parallel Axis Theorem
The parallel axis theorem states that the moment of inertia of a body about any axis is equal to the moment of inertia about a parallel axis through the center of mass plus the product of the mass and the square of the distance between the axes. This theorem is incredibly useful when dealing with objects rotating around an axis that doesn't pass through their center of mass.
Perpendicular Axis Theorem
This theorem applies specifically to planar objects (two-dimensional objects). It states that the moment of inertia of a planar lamina about an axis perpendicular to the plane is equal to the sum of the moments of inertia about any two mutually perpendicular axes in the plane that intersect at the point where the perpendicular axis passes through the plane.
Conservation of Angular Momentum
A significant consequence of Newton's second law for rotational motion is the conservation of angular momentum. If the net external torque acting on a system is zero, the total angular momentum of the system remains constant. This principle is crucial in various phenomena.
For instance, a figure skater spinning faster when they pull their arms closer to their body is a direct consequence of angular momentum conservation. As the moment of inertia decreases (by pulling in arms), the angular velocity must increase to maintain a constant angular momentum.
Beyond the Basics: Advanced Concepts
While τ = Iα provides a fundamental understanding of rotational dynamics, more advanced concepts build upon this foundation. These include:
-
Rotational Kinetic Energy: The energy associated with rotational motion is given by ½Iω². This energy is directly related to the moment of inertia and angular velocity.
-
Precession: The slow, conical rotation of a spinning object subjected to a torque, such as a gyroscope.
-
Nutation: The nodding or wobbling motion often observed in conjunction with precession.
-
Euler's Equations of Motion: These equations describe the rotational motion of a rigid body in a more general setting, considering all three axes of rotation simultaneously.
Conclusion: The Importance of Newton's Second Law for Rotation
Newton's second law for rotational motion, τ = Iα, is a cornerstone of classical mechanics. Its application extends far beyond theoretical physics, impacting engineering design, sports science, and numerous other fields. Understanding the relationships between torque, moment of inertia, and angular acceleration is crucial for analyzing and predicting the motion of rotating objects, leading to advancements and innovations across various disciplines. By mastering this principle and its associated concepts, we unlock a deeper understanding of the world around us.
Latest Posts
Latest Posts
-
The Building Blocks Of Nucleic Acids Are Monomers Called
Mar 31, 2025
-
Can Sample Variance Be Smaller Than Population Variance
Mar 31, 2025
-
Integrated Rate Law For Zero Order Reaction
Mar 31, 2025
-
Is Melting Point Chemical Or Physical
Mar 31, 2025
-
What Is The Difference Between Density Dependent And Density Independent
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Newton's Second Law For Rotational Motion . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
