Integrated Rate Law For Zero Order Reaction
Muz Play
Mar 31, 2025 · 6 min read
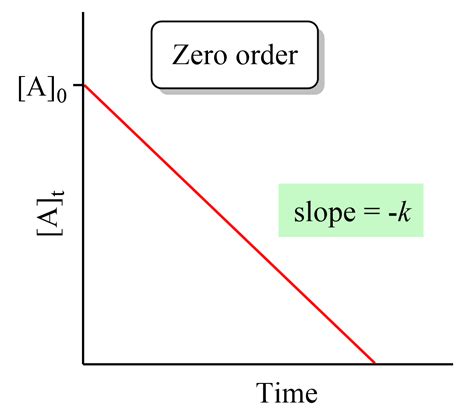
Table of Contents
Integrated Rate Law for Zero-Order Reactions: A Comprehensive Guide
Understanding reaction kinetics is crucial in chemistry and related fields. This detailed guide dives deep into the integrated rate law for zero-order reactions, exploring its derivation, applications, and significance. We will cover everything from the basic concepts to advanced applications, making it a valuable resource for students and professionals alike.
What is a Zero-Order Reaction?
A zero-order reaction is a chemical reaction where the rate of the reaction is independent of the concentration of the reactants. This means that the rate remains constant regardless of how much reactant is present. This seemingly counterintuitive behavior is often observed under specific conditions, which we will explore later.
The rate law for a zero-order reaction is simply:
Rate = k
where:
- Rate represents the rate of the reaction (often expressed in units of M/s or mol L⁻¹ s⁻¹).
- k is the rate constant, a proportionality constant specific to the reaction and temperature. Its units are M/s or mol L⁻¹ s⁻¹.
Deriving the Integrated Rate Law for Zero-Order Reactions
The integrated rate law is obtained by integrating the differential rate law. For a zero-order reaction, the differential rate law is:
d[A]/dt = -k
where [A] represents the concentration of reactant A at time t. The negative sign indicates that the concentration of A decreases over time.
To obtain the integrated rate law, we integrate both sides of the equation with respect to time:
∫d[A] = -k∫dt
Integrating, we get:
[A] = -kt + [A]₀
This is the integrated rate law for a zero-order reaction, where:
- [A] is the concentration of reactant A at time t.
- [A]₀ is the initial concentration of reactant A at time t = 0.
- k is the rate constant.
- t is the time elapsed.
Understanding the Integrated Rate Law Equation
The integrated rate law, [A] = -kt + [A]₀, describes a linear relationship between the concentration of the reactant and time. This is a key characteristic that distinguishes zero-order reactions from other reaction orders. If you plot [A] versus t, you will obtain a straight line with a slope of -k and a y-intercept of [A]₀.
This linear relationship simplifies the analysis of zero-order reactions significantly. Determining the rate constant, k, simply involves finding the slope of the line obtained from a concentration-time plot. The initial concentration, [A]₀, is readily obtained from the y-intercept.
Half-Life of a Zero-Order Reaction
The half-life (t₁/₂) of a reaction is the time it takes for the concentration of the reactant to decrease to half its initial value. For a zero-order reaction, we can derive the half-life by substituting [A] = [A]₀/2 into the integrated rate law:
[A]₀/2 = -kt₁/₂ + [A]₀
Solving for t₁/₂, we get:
t₁/₂ = [A]₀ / 2k
Notice that the half-life of a zero-order reaction is directly proportional to the initial concentration. This is in contrast to first and second-order reactions where the half-life is independent of or inversely proportional to the initial concentration, respectively. This implies that a higher initial concentration of reactant will lead to a longer half-life for a zero-order reaction.
Examples of Zero-Order Reactions
While less common than first or second-order reactions, zero-order reactions do occur under specific conditions. Here are some examples:
-
Enzyme-catalyzed reactions at high substrate concentrations: When the concentration of the substrate is much higher than the concentration of the enzyme, the enzyme becomes saturated. At this point, the rate of the reaction becomes independent of the substrate concentration, exhibiting zero-order kinetics. The enzyme is working at its maximum capacity, and adding more substrate won't increase the rate.
-
Photochemical reactions: In many photochemical reactions, the rate is determined by the intensity of the light source rather than the concentration of the reactants. The light provides the activation energy, and increasing the reactant concentration doesn't affect the rate, resulting in zero-order behavior.
-
Reactions on surfaces: Reactions occurring on surfaces, such as catalytic reactions, can exhibit zero-order kinetics when the surface is saturated with reactants. The rate is then limited by the available surface area rather than the concentration of reactants in the bulk phase.
-
Certain decomposition reactions: Some decomposition reactions can exhibit zero-order kinetics under specific conditions, particularly at high concentrations where the rate is determined by factors other than the reactant concentration.
Determining the Reaction Order Experimentally
Several experimental methods can help determine whether a reaction is zero-order. The most common is by analyzing the concentration-time data:
-
Graphical Method: Plotting the concentration of the reactant ([A]) versus time (t). A straight line with a negative slope indicates a zero-order reaction. The slope of this line is equal to -k.
-
Half-Life Method: Measuring the half-life at different initial concentrations. If the half-life is directly proportional to the initial concentration, the reaction is zero-order.
-
Differential Method: This involves measuring the initial rates of the reaction at different concentrations. If the rate remains constant regardless of the concentration, it points to a zero-order reaction. This method requires careful experimental control and precise measurements.
Applications of Zero-Order Reactions
The understanding of zero-order kinetics is crucial in several areas:
-
Pharmacokinetics: Zero-order kinetics plays a role in understanding drug metabolism and elimination. Some drugs are eliminated from the body at a constant rate, regardless of their concentration, demonstrating zero-order kinetics. This understanding is crucial for determining appropriate dosage regimens.
-
Environmental Chemistry: Zero-order kinetics is applicable in studying the degradation of pollutants in the environment. Understanding the rate of degradation helps in predicting the persistence of pollutants and developing appropriate remediation strategies.
-
Industrial Chemistry: In industrial processes, controlling the reaction rate is essential. Understanding zero-order kinetics can help optimize reaction conditions and maximize product yield.
Limitations and Considerations
While the integrated rate law for zero-order reactions provides a valuable framework, it's crucial to remember its limitations:
-
Idealized Model: Zero-order kinetics is often an idealized model. Real-world reactions may exhibit complex kinetics, deviating from perfect zero-order behavior.
-
Specific Conditions: Zero-order kinetics typically applies only under specific conditions, such as high reactant concentrations or surface saturation, as discussed earlier.
-
Temperature Dependence: The rate constant, k, is temperature-dependent. Changes in temperature can alter the reaction rate and shift the reaction away from zero-order behavior.
Conclusion
The integrated rate law for zero-order reactions, [A] = -kt + [A]₀, is a powerful tool for understanding and analyzing reactions that exhibit this unique kinetic behavior. While less common than other reaction orders, its implications are significant across various fields. By understanding its derivation, applications, and limitations, we can effectively utilize this knowledge to analyze and predict reaction behavior under specific conditions. Mastering the concept of zero-order kinetics provides a solid foundation for delving into more complex reaction mechanisms and kinetic analyses. The ability to distinguish and analyze zero-order reactions is essential for researchers, engineers, and anyone working with chemical processes.
Latest Posts
Latest Posts
-
How To Find Moles Of Naoh Used In Titration
Apr 02, 2025
-
Different Conformations Of The Same Compound
Apr 02, 2025
-
Induced Fit Model Vs Lock And Key
Apr 02, 2025
-
Colligative Properties Freezing Point Depression Lab
Apr 02, 2025
-
Matrix As A Product Of Elementary Matrices
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Integrated Rate Law For Zero Order Reaction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
