Number Of Atoms In A Simple Cubic Unit Cell
Muz Play
Apr 02, 2025 · 5 min read
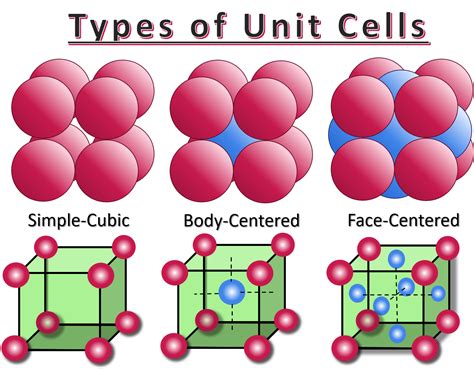
Table of Contents
Determining the Number of Atoms in a Simple Cubic Unit Cell: A Comprehensive Guide
Understanding crystal structures is fundamental in materials science, chemistry, and physics. One of the first concepts encountered is the unit cell, the smallest repeating unit that constitutes a crystal lattice. This article delves into the specifics of determining the number of atoms within a simple cubic unit cell, providing a detailed explanation with accompanying diagrams and examples. We'll also touch upon the broader context of unit cells and their importance in materials characterization.
What is a Unit Cell?
A unit cell is the smallest repeating structural unit of a crystal lattice. Think of it as a building block that, when replicated in three dimensions, generates the entire crystal structure. Different crystal structures are characterized by the arrangement of atoms within their unit cells. Several common unit cell types exist, including simple cubic, body-centered cubic (BCC), face-centered cubic (FCC), and hexagonal close-packed (HCP). Each possesses a unique arrangement of atoms and, consequently, a different number of atoms per unit cell.
The Simple Cubic Unit Cell: A Closer Look
The simple cubic (SC) unit cell is the simplest arrangement. Atoms are located only at the corners of the cube. This seemingly simple structure provides a crucial foundation for understanding more complex crystal structures. While less common in nature compared to BCC and FCC structures, understanding the SC unit cell is crucial for grasping fundamental crystallographic principles.
Visualizing the Simple Cubic Unit Cell
Imagine a cube. In a simple cubic unit cell, each corner of this cube is occupied by a single atom. These corner atoms are shared between adjacent unit cells. This sharing is a key aspect when calculating the total number of atoms within a single unit cell. Let's visualize this with a simple diagram:
A
/|\
/ | \
A--A--A
| | |
| | |
A--A--A
A
In this representation, 'A' represents an atom located at the corner of the cube.
Calculating the Number of Atoms in a Simple Cubic Unit Cell
The crucial point to remember when calculating the number of atoms within a unit cell is that atoms located at the corners are shared between multiple adjacent unit cells. Each corner atom is shared by eight adjacent unit cells.
Therefore, the contribution of each corner atom to a single unit cell is only 1/8. Since there are eight corners in a cube, the total number of atoms from the corner positions is:
(1/8 atom/corner) * 8 corners = 1 atom
Therefore, a simple cubic unit cell contains only one atom.
Beyond the Simple Cubic Unit Cell: Other Crystal Structures
Understanding the simple cubic unit cell is a springboard to comprehending more complex structures. Let's briefly compare it with other common crystal structures:
-
Body-Centered Cubic (BCC): In addition to the eight corner atoms (contributing 1 atom), a BCC unit cell has one atom located at the center of the cube. Therefore, a BCC unit cell contains a total of two atoms.
-
Face-Centered Cubic (FCC): An FCC unit cell has eight corner atoms (contributing 1 atom) and six face-centered atoms. Each face-centered atom is shared by two unit cells, contributing 1/2 an atom per face. With six faces, this contributes (1/2 atom/face) * 6 faces = 3 atoms. Thus, an FCC unit cell contains a total of four atoms (1 + 3 = 4).
-
Hexagonal Close-Packed (HCP): The HCP structure is slightly more complex, involving a hexagonal base. It contains a total of six atoms per unit cell, a result derived from a more involved geometrical analysis.
Applications and Significance
The knowledge of unit cells and the number of atoms they contain is crucial in various fields:
-
Materials Science: Determining the number of atoms in a unit cell is essential for calculating density, calculating the distance between atoms, predicting material properties, and understanding phase transformations. For instance, the density of a material is directly related to the number of atoms within its unit cell and its atomic weight.
-
X-ray Crystallography: X-ray diffraction patterns from crystalline materials provide information about the arrangement of atoms within the unit cell. The number of atoms and their positions within the unit cell are critical parameters in interpreting these diffraction patterns.
-
Solid-State Physics: Understanding crystal structure is pivotal in explaining many physical properties, such as electrical conductivity, magnetic properties, and thermal conductivity. The arrangement of atoms within the unit cell significantly impacts these properties.
-
Chemistry: Crystalline solids represent a significant portion of chemical compounds. Knowing the unit cell structure and the number of atoms per unit cell is crucial for understanding the chemical bonding, reactivity, and other chemical behaviors of substances.
Further Exploration: Atomic Packing Factor (APF)
The Atomic Packing Factor (APF) is a measure of how efficiently atoms are packed within a unit cell. It's defined as the ratio of the volume of atoms within the unit cell to the total volume of the unit cell.
For a simple cubic unit cell, the APF is relatively low at approximately 0.52. This indicates that there's significant empty space within the structure, which explains why the simple cubic structure is less prevalent than others with higher APFs, such as FCC (0.74) and HCP (0.74).
Conclusion
Determining the number of atoms in a simple cubic unit cell, while seemingly a simple calculation, provides a foundational understanding of crystallography and its applications. The principles applied here extend to more complex crystal structures, emphasizing the importance of recognizing the shared nature of atoms within unit cells and their contribution to the overall count. This understanding forms a critical cornerstone for comprehending a wide array of material properties and behaviors across diverse scientific disciplines. The concept is not only crucial for academic pursuits but also has significant implications in material design and technological advancements. Further investigation into other crystal structures and the calculation of atomic packing factors will deepen your grasp of the rich world of crystallography.
Latest Posts
Latest Posts
-
Energy Flow In Plants Concept Map
Apr 03, 2025
-
Chondrocytes Are To Cartilage As Osteocytes Are To
Apr 03, 2025
-
What Is The Dielectric Constant Of Water
Apr 03, 2025
-
Draw A Phasor Diagram Showing Generator Voltage At Time 0
Apr 03, 2025
-
What Is A Wet Mount Slide
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Number Of Atoms In A Simple Cubic Unit Cell . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
