Quantum Mechanical Model Vs Bohr Model
Muz Play
Apr 05, 2025 · 6 min read
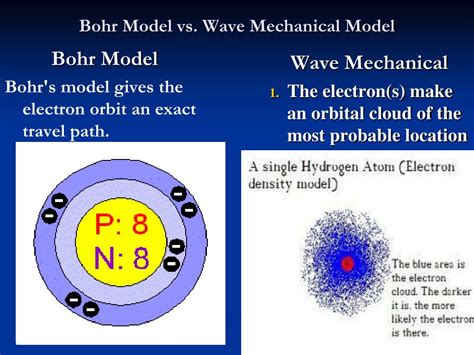
Table of Contents
Quantum Mechanical Model vs. Bohr Model: A Deep Dive into Atomic Structure
The atom, the fundamental building block of matter, has captivated scientists for centuries. Our understanding of its structure has evolved dramatically, moving from simple models to increasingly sophisticated ones that reflect the complexities of quantum mechanics. Two pivotal models stand out in this historical journey: the Bohr model and the quantum mechanical model. While the Bohr model provided a significant advancement in its time, the quantum mechanical model offers a far more accurate and comprehensive representation of atomic behavior. This article delves into a detailed comparison of these two models, highlighting their strengths, weaknesses, and the fundamental differences that set them apart.
The Bohr Model: A Stepping Stone to Understanding
Proposed by Niels Bohr in 1913, the Bohr model revolutionized atomic theory. Before Bohr, the prevailing picture of the atom was a largely undefined structure with electrons embedded within a positively charged sphere (the plum pudding model). Bohr introduced a revolutionary concept: electrons orbit the nucleus in specific energy levels. This model incorporated quantization, a concept that suggested that energy is not continuous but exists in discrete packets or quanta.
Key Features of the Bohr Model:
- Quantized Orbits: Electrons revolve around the nucleus in fixed, circular orbits with specific energy levels. These energy levels are quantized, meaning electrons can only exist in these specific orbits and not in between.
- Energy Level Transitions: Electrons can transition between energy levels by absorbing or emitting photons of light. The energy of the photon corresponds exactly to the energy difference between the two levels. This elegantly explained the discrete line spectra observed in atomic emissions.
- Ground State: Electrons occupy the lowest energy level (ground state) unless they absorb energy and jump to a higher energy level (excited state).
- Stable Orbits: The model postulated that electrons in these specific orbits do not radiate energy, thereby avoiding the collapse of the atom predicted by classical physics.
Limitations of the Bohr Model:
Despite its success in explaining the hydrogen spectrum, the Bohr model possessed several significant limitations:
- Inaccurate for Multi-electron Atoms: It failed to accurately predict the spectra of atoms with more than one electron. The interactions between multiple electrons were not accounted for, leading to discrepancies between theoretical predictions and experimental observations.
- Inadequate Explanation of Fine Structure: The model could not explain the fine structure of spectral lines – slight splitting of spectral lines observed under high resolution.
- Failed to Predict Chemical Bonding: It offered no explanation for the formation of chemical bonds or the behavior of molecules.
- Inconsistent with Heisenberg's Uncertainty Principle: The Bohr model assumes electrons have both a definite position and momentum, contradicting the Heisenberg uncertainty principle which states that it's impossible to know both with perfect accuracy.
- Could not explain the Zeeman effect: The model failed to account for the splitting of spectral lines in the presence of a magnetic field (Zeeman effect).
The Quantum Mechanical Model: A More Accurate Representation
The quantum mechanical model, developed in the 1920s, offers a significantly more accurate and complete description of the atom. It builds upon the concepts of quantization but incorporates the wave-particle duality of matter, described by de Broglie's hypothesis, and the Heisenberg uncertainty principle. Instead of treating electrons as particles orbiting the nucleus in well-defined paths, this model utilizes wave functions to describe the probability of finding an electron in a particular region of space.
Key Features of the Quantum Mechanical Model:
- Wave-Particle Duality: Electrons exhibit both wave-like and particle-like properties. This duality is incorporated using Schrödinger's equation, which treats electrons as wave functions.
- Orbitals: Instead of orbits, the quantum mechanical model introduces the concept of atomic orbitals. These are regions in space where there is a high probability of finding an electron. Each orbital is characterized by a set of quantum numbers.
- Quantum Numbers: Four quantum numbers describe the state of an electron:
- Principal Quantum Number (n): Determines the energy level and size of the orbital (n = 1, 2, 3...).
- Azimuthal Quantum Number (l): Determines the shape of the orbital (l = 0, 1, 2... n-1). l=0 corresponds to s orbitals (spherical), l=1 to p orbitals (dumbbell-shaped), l=2 to d orbitals, and so on.
- Magnetic Quantum Number (ml): Determines the orientation of the orbital in space (ml = -l, -l+1... 0... l-1, l).
- Spin Quantum Number (ms): Describes the intrinsic angular momentum of the electron (ms = +1/2 or -1/2). This indicates the electron's spin, either "up" or "down".
- Electron Configuration: The arrangement of electrons in different orbitals is described by the electron configuration. The Aufbau principle, Hund's rule, and the Pauli exclusion principle guide the filling of orbitals.
- Probability Density: The square of the wave function gives the probability density of finding an electron at a specific point in space. This means we can't pinpoint an electron's exact location, but we can determine the probability of it being in a specific region.
- Quantum Superposition: Before measurement, an electron can exist in a superposition of states, occupying multiple orbitals simultaneously. Only upon measurement does it collapse into a single state.
Advantages of the Quantum Mechanical Model:
- Accuracy: It provides a much more accurate description of atomic spectra and other atomic properties than the Bohr model.
- Applicability to Multi-electron Atoms: The quantum mechanical model successfully accounts for the interactions between multiple electrons and accurately predicts the spectra of multi-electron atoms.
- Explanation of Chemical Bonding: It explains the formation of chemical bonds and the properties of molecules through concepts like molecular orbitals and valence bond theory.
- Compatibility with Quantum Mechanics: The model is fully consistent with the principles of quantum mechanics, including the wave-particle duality and the Heisenberg uncertainty principle.
- Explains Fine Structure and Zeeman Effect: It successfully explains the fine structure of spectral lines and the Zeeman effect.
A Direct Comparison: Bohr vs. Quantum Mechanical Model
| Feature | Bohr Model | Quantum Mechanical Model |
|---|---|---|
| Electron Description | Particles in fixed circular orbits | Wave functions describing probability density |
| Energy Levels | Quantized energy levels | Quantized energy levels, but more complex |
| Electron Location | Precisely defined orbit | Probability distribution within an orbital |
| Multi-electron Atoms | Fails to accurately predict spectra | Accurately predicts spectra |
| Chemical Bonding | No explanation | Explains chemical bonding |
| Uncertainty Principle | Violates the uncertainty principle | Consistent with the uncertainty principle |
| Spectra | Explains the hydrogen spectrum | Explains the spectra of all atoms |
| Mathematical Complexity | Relatively simple | Significantly more complex |
| Accuracy | Limited accuracy | High accuracy |
Conclusion: The Quantum Mechanical Model Triumphs
The Bohr model served as a crucial stepping stone in our understanding of atomic structure. Its simplicity made it a valuable teaching tool and it successfully explained certain aspects of the hydrogen atom’s behavior. However, its limitations became apparent as our understanding of quantum mechanics deepened.
The quantum mechanical model, although far more complex mathematically, provides a far more accurate and complete picture of atomic behavior. It accounts for the wave-particle duality of electrons, predicts the spectra of all atoms, explains chemical bonding, and is consistent with the fundamental principles of quantum mechanics. It remains the cornerstone of modern atomic theory, allowing us to understand and predict a vast range of phenomena in chemistry and physics. While the Bohr model remains a valuable historical artifact, the quantum mechanical model stands as a testament to the power and accuracy of quantum theory in explaining the intricacies of the atomic world.
Latest Posts
Latest Posts
-
Which Is Smaller An Atom Or A Molecule
Apr 05, 2025
-
Stopping A Filibuster Requires That
Apr 05, 2025
-
What Are The Two Major Divisions Of The Skeletal System
Apr 05, 2025
-
Delta S Delta H Delta G Chart
Apr 05, 2025
-
How Many Unpaired Electrons Does Sulfur Have
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Quantum Mechanical Model Vs Bohr Model . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
