Rate Law For Iodine Clock Reaction
Muz Play
Mar 28, 2025 · 6 min read
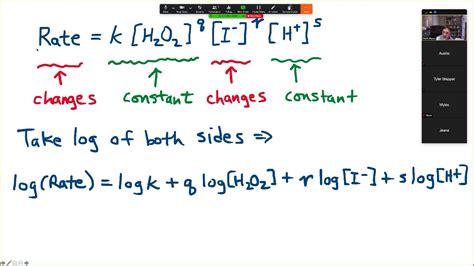
Table of Contents
Rate Law for the Iodine Clock Reaction: A Comprehensive Guide
The iodine clock reaction is a classic chemistry experiment demonstrating the principles of chemical kinetics and reaction rates. Its dramatic visual change – a sudden appearance of a deep blue-black color – makes it a captivating way to study reaction mechanisms and determine rate laws. This comprehensive guide will delve into the intricacies of the iodine clock reaction, focusing on how to determine its rate law.
Understanding the Iodine Clock Reaction
The iodine clock reaction typically involves the oxidation of iodide ions (I⁻) by hydrogen peroxide (H₂O₂) in an acidic solution. This reaction, however, is not directly observable. Instead, the reaction produces iodine (I₂), which then reacts with starch to form a dark blue-black complex. This color change serves as a "clock," marking the point at which a certain concentration of iodine has been produced. The time it takes for this color change to occur is directly related to the reaction rate.
The overall reaction can be simplified as follows:
H₂O₂ + 2I⁻ + 2H⁺ → I₂ + 2H₂O
However, this is often not a simple one-step process. The actual mechanism is more complex and usually involves several elementary steps. Understanding this mechanism is crucial for accurately determining the rate law.
Determining the Rate Law: Experimental Approach
The rate law expresses the relationship between the reaction rate and the concentrations of the reactants. For a general reaction aA + bB → products, the rate law is typically expressed as:
Rate = k[A]ˣ[B]ʸ
where:
- k is the rate constant (temperature-dependent)
- [A] and [B] are the concentrations of reactants A and B
- x and y are the reaction orders with respect to A and B, respectively. These are not necessarily equal to the stoichiometric coefficients (a and b). They must be determined experimentally.
To determine the rate law for the iodine clock reaction, we employ a method of initial rates. This involves conducting several experiments, varying the initial concentrations of the reactants while keeping other factors (temperature, volume) constant. By comparing the initial rates of reaction under these different conditions, we can deduce the reaction orders (x and y).
The Experimental Procedure: A Step-by-Step Guide
-
Prepare Solutions: Prepare solutions of H₂O₂, KI, H₂SO₄ (or another suitable acid), and starch solution at known concentrations. The concentration of starch is usually significantly lower than the concentrations of the other reactants.
-
Set up the Experiment: Use several separate beakers or flasks to prepare separate solutions containing the different reactants. In separate vessels mix a mixture of I⁻, H⁺ (acid), and starch. In a second vessel prepare a H₂O₂ solution.
-
Initiate the Reaction: Quickly combine the two solutions, initiating the reaction. Start a stopwatch simultaneously.
-
Measure the Time: Observe and record the time it takes for the characteristic blue-black color to appear, indicating a measurable concentration of I₂. This time is inversely proportional to the initial rate; shorter times indicate faster rates.
-
Vary Concentrations: Repeat steps 2-4, varying the initial concentrations of one reactant at a time while keeping the others constant. Ideally, you'd systematically vary the concentration of H₂O₂ and then I⁻, keeping the other concentrations and the acid concentration constant each time.
-
Data Analysis: Use the collected data (initial concentrations and reaction times) to calculate the initial rates for each experiment. Then, using the method of initial rates, determine the reaction orders with respect to H₂O₂ and I⁻. This usually involves comparing rates from experiments where only one concentration is changed. For example, if doubling the concentration of H₂O₂ doubles the rate, the reaction order with respect to H₂O₂ is 1. If doubling the concentration quadruples the rate, the reaction order is 2.
Data Interpretation and Rate Law Determination
Once you have the initial rates from several experiments, you can mathematically determine the reaction orders. Here's a typical approach:
Let's assume we have three experiments:
- Experiment 1: [H₂O₂] = A, [I⁻] = B, Rate = R₁
- Experiment 2: [H₂O₂] = 2A, [I⁻] = B, Rate = R₂
- Experiment 3: [H₂O₂] = A, [I⁻] = 2B, Rate = R₃
To find the order with respect to [H₂O₂]:
(R₂/R₁) = (k(2A)ˣ(B)ʸ)/(k(A)ˣ(B)ʸ) = 2ˣ
Solving for x gives the order with respect to H₂O₂.
Similarly, to find the order with respect to [I⁻]:
(R₃/R₁) = (k(A)ˣ(2B)ʸ)/(k(A)ˣ(B)ʸ) = 2ʸ
Solving for y gives the order with respect to I⁻.
Once both x and y are determined, substitute them, along with the rate constant k (obtained from one of the experiments), into the rate law equation:
Rate = k[H₂O₂]ˣ[I⁻]ʸ
This equation describes the relationship between the reaction rate and the concentrations of the reactants for the iodine clock reaction under the specific conditions of the experiment.
Factors Affecting the Rate Law
Several factors can influence the rate law, even if the overall reaction remains the same:
-
Temperature: An increase in temperature generally increases the rate constant (k), leading to a faster reaction rate. This is due to increased kinetic energy of the reactant molecules.
-
Ionic Strength: The presence of other ions in the solution can affect the rate of reaction through ionic strength effects.
-
Catalyst: Adding a catalyst can alter the reaction mechanism and therefore the rate law. The catalyst provides an alternative pathway with a lower activation energy.
-
pH: The acidity (pH) of the solution affects the reaction rate. In this case, hydrogen ion concentration directly impacts the reaction rate. Different pH values might lead to variations in reaction orders, as different reaction steps become rate-determining.
Advanced Considerations and Complexities
The iodine clock reaction's apparent simplicity can be deceiving. The actual reaction mechanism is more complicated than the single overall reaction equation suggests. It often involves several intermediate steps, and identifying the rate-determining step is critical for an accurate understanding of the rate law. Additional intermediate species may impact the observed rate. Advanced techniques, including spectroscopic measurements, can provide more detailed information about the reaction mechanism and identify these intermediate steps.
Conclusion: A Powerful Tool for Kinetic Studies
The iodine clock reaction provides a compelling and visually engaging method for studying chemical kinetics and determining rate laws. While determining the rate law involves careful experimental design and rigorous data analysis, the inherent visual feedback and relatively straightforward procedure make it a valuable tool for both introductory and advanced chemistry education. A deeper understanding of the factors influencing the rate, coupled with proper experimental technique and data interpretation, provides a firm foundation in chemical kinetics. Remember that the rate law obtained is only valid under the specific experimental conditions employed. Varying conditions necessitates re-determination.
Latest Posts
Latest Posts
-
What Is The Electron Configuration Of Beryllium
Mar 31, 2025
-
When Do You Consider Log Diterminants Similar
Mar 31, 2025
-
Find The Rectangular Equation And Eliminate The Parameters
Mar 31, 2025
-
How To Calculate The Enthalpy Of Fusion
Mar 31, 2025
-
How Does Meiosis Generate Genetic Diversity
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Rate Law For Iodine Clock Reaction . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
