What Are Signed Numbers In Math
Muz Play
Mar 28, 2025 · 6 min read
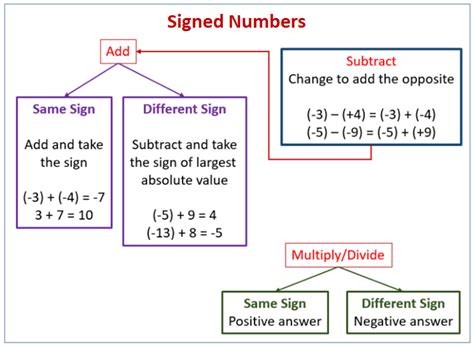
Table of Contents
What Are Signed Numbers in Math? A Comprehensive Guide
Signed numbers are a fundamental concept in mathematics that extends the number system beyond the familiar positive integers (1, 2, 3...) to include their negative counterparts (-1, -2, -3...) and zero (0). Understanding signed numbers is crucial for tackling more advanced mathematical concepts and real-world applications. This comprehensive guide will explore signed numbers in detail, covering their representation, operations, applications, and importance in various fields.
Understanding the Number Line
The easiest way to visualize signed numbers is through the number line. The number line is a visual representation of numbers extending infinitely in both positive and negative directions.
- Zero (0): The central point on the number line, representing neither positive nor negative value.
- Positive Numbers: Numbers located to the right of zero, denoted with a "+" sign (although often omitted). For instance, +5 is the same as 5.
- Negative Numbers: Numbers located to the left of zero, denoted with a "-" sign. For example, -3 represents three units to the left of zero.
This simple representation helps understand the relative magnitude and position of signed numbers. For example, -2 is less than 0, and 3 is greater than -5.
Representing Signed Numbers
Signed numbers can be represented in several ways:
- Using "+" and "-" signs: The most common method, directly indicating whether the number is positive or negative. Examples: +7, -2, 0.
- In Context: Sometimes, the context itself indicates the sign. For example, a bank balance of -$50 clearly indicates a negative balance. A temperature of 10°C suggests a positive temperature.
- On a Coordinate Plane: In two or three dimensions, signed numbers are used to represent coordinates, indicating the position of a point relative to the origin.
Operations with Signed Numbers
Performing arithmetic operations (addition, subtraction, multiplication, and division) with signed numbers requires understanding specific rules:
1. Addition of Signed Numbers
- Adding numbers with the same sign: Add their absolute values and keep the common sign. For example, -3 + (-5) = -8; 4 + 6 = 10.
- Adding numbers with different signs: Subtract the smaller absolute value from the larger absolute value. The result takes the sign of the number with the larger absolute value. For example, 7 + (-3) = 4; -9 + 5 = -4.
2. Subtraction of Signed Numbers
Subtraction of a signed number is the same as adding its opposite. This means changing the sign of the number being subtracted and then adding.
- Example 1: 5 - 3 = 5 + (-3) = 2
- Example 2: -2 - 7 = -2 + (-7) = -9
- Example 3: -4 - (-6) = -4 + 6 = 2
3. Multiplication and Division of Signed Numbers
- Multiplying or dividing numbers with the same sign: The result is positive. For example, (-5) * (-3) = 15; 6 / 2 = 3.
- Multiplying or dividing numbers with different signs: The result is negative. For example, (-4) * 2 = -8; 10 / (-5) = -2.
These rules are consistent and allow for accurate calculations involving signed numbers.
Absolute Value
The absolute value of a number is its distance from zero on the number line, always expressed as a non-negative number. It's denoted by vertical bars: | |.
- Examples: |5| = 5; |-5| = 5; |0| = 0.
Absolute value is frequently used in various mathematical operations and problem-solving scenarios.
Applications of Signed Numbers
Signed numbers are not just abstract mathematical concepts; they have widespread applications in various fields:
1. Temperature Measurement:
Temperature scales like Celsius and Fahrenheit use signed numbers to represent temperatures below and above zero.
2. Finance:
Signed numbers are essential in representing profits and losses, bank balances (credits and debits), and stock market fluctuations.
3. Elevation and Depth:
Signed numbers describe elevations above and below sea level, allowing for accurate representation of geographical features.
4. Physics and Engineering:
Signed numbers are critical in representing vectors (quantities with both magnitude and direction), forces (push and pull), and velocities (speed and direction).
5. Computer Science:
Signed numbers are fundamental in computer programming and data representation, influencing how data is stored and processed. For example, representing positive and negative integers within memory requires understanding signed number representations.
6. Chemistry:
In chemical reactions, signed numbers can represent oxidation states, indicating the charge of atoms.
7. Accounting:
Signed numbers are fundamental in accounting for assets, liabilities, income and expenses. Debits and credits are expressed using signed numbers and are essential for balancing accounting records.
Advanced Concepts Involving Signed Numbers
Beyond the basic operations, several advanced concepts utilize signed numbers:
-
Order of Operations (PEMDAS/BODMAS): When dealing with multiple operations, the order of operations (Parentheses/Brackets, Exponents/Orders, Multiplication and Division, Addition and Subtraction) must be strictly followed, even with signed numbers.
-
Inequalities: Signed numbers are essential when dealing with inequalities (<, >, ≤, ≥). For instance, -3 < 2 and -5 > -10.
-
Coordinate Geometry: Signed numbers are crucial for defining coordinates in Cartesian planes (2D) and Cartesian spaces (3D), allowing for the precise location of points and the calculation of distances and areas.
-
Vectors: As mentioned previously, signed numbers are fundamental in defining and working with vectors, which have both magnitude and direction.
-
Matrices and Determinants: Matrices often contain signed numbers, and their manipulation involves operations with signed numbers. The determinants of matrices are also often signed numbers that reveal essential information about the matrix.
Solving Problems with Signed Numbers
Solving problems involving signed numbers requires careful application of the rules outlined above and a strong understanding of the context. Here's a step-by-step approach:
-
Identify the signed numbers: Clearly identify all the positive and negative numbers in the problem.
-
Understand the operations: Determine the arithmetic operations involved (addition, subtraction, multiplication, division).
-
Apply the rules: Follow the rules for adding, subtracting, multiplying, and dividing signed numbers correctly.
-
Order of operations: If multiple operations are involved, strictly adhere to the order of operations (PEMDAS/BODMAS).
-
Interpret the result: The final answer should be interpreted in the context of the problem. For example, a negative result in a financial problem might represent a loss.
Conclusion
Signed numbers are a cornerstone of mathematics, extending the number system to encompass negative values and zero. Their importance extends far beyond theoretical calculations; they are essential tools in diverse fields, from finance and temperature measurement to physics and computer science. A thorough understanding of their representation, operations, and applications is crucial for anyone seeking to master mathematics and its practical implications. By understanding the rules governing their operations and applying them methodically, you can confidently tackle various mathematical problems and appreciate their relevance in the real world. Mastering signed numbers is a key stepping stone to more complex mathematical concepts and unlocks the potential to solve a wider array of problems in diverse fields.
Latest Posts
Latest Posts
-
What Is The Basic Unit Of Measurement
Mar 31, 2025
-
Is It Possible To Love 2 People At Once
Mar 31, 2025
-
What Does The Atomic Mass Of An Element Represent
Mar 31, 2025
-
Electric Field Of A Charged Disk
Mar 31, 2025
-
5 Blind Man And The Elephant
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Are Signed Numbers In Math . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
