What Does Disjoint Mean In Probability
Muz Play
Mar 29, 2025 · 7 min read
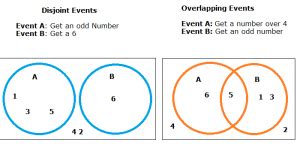
Table of Contents
What Does Disjoint Mean in Probability? A Comprehensive Guide
Understanding the concept of disjoint events is fundamental to mastering probability. Disjoint events, also known as mutually exclusive events, play a crucial role in various probability calculations and are essential for grasping more complex probabilistic concepts. This comprehensive guide will delve deep into the meaning of disjoint events, exploring their characteristics, providing illustrative examples, and showcasing their applications in different scenarios. We'll also examine how they differ from independent events and how to identify them in various probability problems.
Understanding Disjoint Events: The Basics
In the realm of probability, disjoint events are defined as events that cannot occur simultaneously. This means that if one event occurs, the other event cannot occur. There's no overlap between these events; they are completely separate from each other. Think of it like flipping a coin: you can either get heads or tails, but you cannot get both at the same time. These are classic examples of disjoint events.
Key Characteristics of Disjoint Events:
- Mutual Exclusivity: This is the core characteristic. The occurrence of one event automatically excludes the possibility of the other event happening.
- No Overlap: The events share no common outcomes. Their sets of possible outcomes are completely distinct.
- Probability of Intersection is Zero: The probability of both events occurring simultaneously (represented as P(A ∩ B), where A and B are the events) is always zero. This is a mathematical consequence of their mutual exclusivity.
Visualizing Disjoint Events
A Venn diagram is a powerful tool for visualizing disjoint events. In a Venn diagram, each event is represented by a circle. If the circles do not overlap at all, it visually represents disjoint events.
[Imagine a Venn Diagram here showing two circles, A and B, with no overlap.]
In this diagram, the circles representing events A and B are completely separate. There is no area of intersection, illustrating the absence of any shared outcomes.
Examples of Disjoint Events
Let's look at some concrete examples to solidify our understanding:
- Rolling a Die: The event of rolling a 3 and the event of rolling a 6 are disjoint. You cannot roll a 3 and a 6 simultaneously on a single roll of a fair six-sided die.
- Drawing Cards: Drawing a King and drawing a Queen from a standard deck of cards (without replacement) are disjoint events. Once you draw a King, you can't draw a Queen on the same draw.
- Weather Conditions: The event of it raining and the event of it being sunny at the same time and place are disjoint. It cannot be both raining and sunny concurrently in the same location.
- Gender: The event of a person being male and the event of a person being female (considering only binary genders for simplicity) are disjoint. A person cannot be both male and female simultaneously.
- Survey Responses: In a survey asking about favorite colors, selecting "blue" and selecting "green" are disjoint events (assuming respondents can only choose one favorite color).
Distinguishing Disjoint Events from Independent Events
It's crucial to distinguish between disjoint events and independent events. While seemingly similar, they represent distinct concepts.
Independent Events: Two events are independent if the occurrence of one event does not affect the probability of the other event occurring. For example, flipping a coin twice: the outcome of the first flip (heads or tails) does not influence the outcome of the second flip. The events are independent.
The Key Difference: Disjoint events cannot occur together, while independent events can occur together (and their probabilities are multiplied to find the probability of both happening). The crucial distinction lies in the relationship between the occurrence of one event and the possibility of the other event's occurrence.
Consider this: The events of rolling a 3 and rolling an even number on a six-sided die are not disjoint (because rolling a 3 is not mutually exclusive with rolling an even number, if you allow the definition of ‘rolling an even number’ to include any even number). However, they are not independent either, since the probability of rolling an even number changes if you know you've already rolled a 3.
Calculating Probabilities with Disjoint Events
The probability of either of two disjoint events occurring is simply the sum of their individual probabilities. This is formally stated as:
P(A ∪ B) = P(A) + P(B) (for disjoint events A and B)
where:
- P(A ∪ B) represents the probability of event A or event B occurring.
- P(A) represents the probability of event A occurring.
- P(B) represents the probability of event B occurring.
This formula simplifies probability calculations significantly when dealing with mutually exclusive events. You don't need to worry about subtracting the probability of the intersection (since it's zero).
Example:
What is the probability of rolling a 1 or a 6 on a fair six-sided die?
- P(rolling a 1) = 1/6
- P(rolling a 6) = 1/6
- Since these are disjoint events, P(rolling a 1 or a 6) = P(rolling a 1) + P(rolling a 6) = 1/6 + 1/6 = 2/6 = 1/3
Applications of Disjoint Events in Real-World Scenarios
The concept of disjoint events finds applications in various fields, including:
- Risk Assessment: In financial modeling and risk management, disjoint events are used to analyze potential risks. For instance, assessing the probability of different types of financial crises occurring (e.g., credit crunch, inflation shock).
- Quality Control: In manufacturing, the probability of different types of defects occurring in a product can be modeled as disjoint events.
- Medical Diagnosis: The probabilities of different diseases causing similar symptoms can sometimes be treated as disjoint events (though this depends heavily on the specifics of the situation).
- Actuarial Science: In insurance, modeling different types of claims (e.g., car accidents, home fires) often involves considering disjoint events to assess risk.
- Machine Learning: Disjoint events are used to define distinct classes in classification problems.
Extending to More Than Two Disjoint Events
The principle of adding probabilities for disjoint events extends to any number of events. If you have n mutually exclusive events A₁, A₂, ..., Aₙ, then the probability of at least one of them occurring is:
P(A₁ ∪ A₂ ∪ ... ∪ Aₙ) = P(A₁) + P(A₂) + ... + P(Aₙ)
This formula is extremely useful when dealing with multiple possibilities that cannot happen simultaneously.
Addressing Complex Scenarios with Partitions
A partition of a sample space is a collection of disjoint events that cover the entire sample space. This means that every outcome in the sample space belongs to exactly one of the events in the partition. Partitions are especially helpful when analyzing probabilities of complex scenarios.
Example:
Consider the experiment of rolling a six-sided die. The events {1}, {2}, {3}, {4}, {5}, {6} form a partition of the sample space. Each outcome (rolling a 1, 2, 3, 4, 5, or 6) belongs to exactly one of these events. They are mutually exclusive (you can't roll two numbers simultaneously), and their union encompasses all possible outcomes.
Dealing with Non-Disjoint Events: The Inclusion-Exclusion Principle
When events are not disjoint (they have overlapping outcomes), we cannot simply add their probabilities. In such cases, we use the inclusion-exclusion principle:
P(A ∪ B) = P(A) + P(B) - P(A ∩ B)
Here, P(A ∩ B) represents the probability of both A and B occurring. This formula corrects for double-counting the overlapping outcomes. This principle is essential when dealing with events that are not mutually exclusive. The inclusion-exclusion principle can be generalized to more than two events, but the formula becomes increasingly complex with more events.
Conclusion: Mastering Disjoint Events in Probability
Understanding the concept of disjoint events is crucial for developing a strong foundation in probability. Their characteristics, their distinction from independent events, and the methods for calculating probabilities involving disjoint events are fundamental tools in various fields. By grasping the core principles and applying them to real-world scenarios, you can significantly improve your ability to model and analyze uncertain situations. From simple coin flips to complex risk assessments, the concept of disjointness is a cornerstone of probabilistic reasoning. Remember that visualizing events using Venn diagrams can be a valuable aid in understanding whether events are disjoint or not. The ability to identify disjoint events will allow for easier probability calculations and a stronger understanding of probabilistic relationships.
Latest Posts
Latest Posts
-
What Are The Factors In An Experiment
Apr 01, 2025
-
What Is In The Cranial Cavity
Apr 01, 2025
-
Lab Skills Using A Graduated Cylinder
Apr 01, 2025
-
Which Molecules In Eukaryotic Cells Regulate Gene Expression
Apr 01, 2025
-
How Do Natural Killer Cells Destroy Invading Pathogens
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about What Does Disjoint Mean In Probability . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
