What Is A Signed Number In Math
Muz Play
Apr 06, 2025 · 5 min read
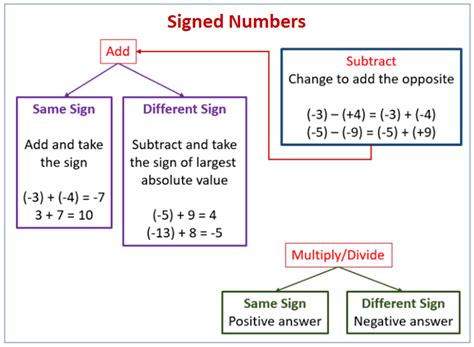
Table of Contents
What is a Signed Number in Math? A Comprehensive Guide
Signed numbers are a fundamental concept in mathematics, representing values that possess both magnitude (size) and direction (sign). Understanding signed numbers is crucial for progressing in various mathematical fields, including algebra, calculus, and even more advanced concepts. This comprehensive guide will explore the intricacies of signed numbers, their representation, operations, and practical applications.
Understanding the Concept of Sign
The "sign" of a number signifies its position relative to zero on the number line. A positive number (+ or no sign indicated) lies to the right of zero, while a negative number (-) lies to the left of zero. Zero itself is neither positive nor negative; it's the point of separation between positive and negative numbers.
Think of a number line as a visual representation of signed numbers:
-3 -2 -1 0 1 2 3
Here, -3 is a negative number, 0 is zero, and 3 is a positive number. The further a number is from zero, the greater its magnitude (or absolute value).
The Importance of Context
The context in which a signed number is used is vital to its interpretation. For instance:
- Temperature: -5°C represents a temperature of 5 degrees Celsius below zero.
- Altitude: -100 meters signifies a point 100 meters below sea level.
- Finance: -$50 indicates a debt of $50.
- Coordinates: In a coordinate system, negative numbers indicate positions along negative axes (left or down).
Without understanding the context, a signed number is just a symbol; understanding the context gives it meaning and practical application.
Representing Signed Numbers
Signed numbers can be represented in various ways:
-
Plus (+) and Minus (-) Signs: This is the most common method. A plus sign (+) before a number indicates positivity, while a minus sign (-) indicates negativity. For example, +5 (or simply 5) and -5.
-
Number Line: As discussed earlier, a number line provides a visual representation of signed numbers and their relative positions.
-
Coordinate System: In a coordinate system (like the Cartesian plane), signed numbers are used to represent coordinates. For example, the point (-2, 3) represents a location 2 units to the left of the y-axis and 3 units above the x-axis.
Operations with Signed Numbers
Performing operations (addition, subtraction, multiplication, and division) with signed numbers requires careful attention to the signs.
Addition of Signed Numbers
-
Adding Two Positive Numbers: Simply add the numbers together. For example, 5 + 3 = 8.
-
Adding Two Negative Numbers: Add the magnitudes of the numbers and keep the negative sign. For example, -5 + (-3) = -8.
-
Adding a Positive and a Negative Number: Subtract the smaller magnitude from the larger magnitude and keep the sign of the number with the larger magnitude. For example:
- 5 + (-3) = 2
- -5 + 3 = -2
Subtraction of Signed Numbers
Subtraction can be thought of as adding the opposite. To subtract a number, add its additive inverse (opposite).
-
Subtracting a Positive Number: Add the negative of that number. For example, 5 - 3 = 5 + (-3) = 2.
-
Subtracting a Negative Number: Add the positive of that number. For example, 5 - (-3) = 5 + 3 = 8.
-
Subtracting Negative from Negative: Example: -5 - (-3) = -5 + 3 = -2
Multiplication and Division of Signed Numbers
The rules for multiplying and dividing signed numbers are:
- Positive × Positive = Positive (e.g., 3 × 2 = 6)
- Negative × Negative = Positive (e.g., -3 × -2 = 6)
- Positive × Negative = Negative (e.g., 3 × -2 = -6)
- Negative × Positive = Negative (e.g., -3 × 2 = -6)
The same rules apply to division.
Absolute Value
The absolute value of a number is its distance from zero on the number line. It's always non-negative. It's denoted by vertical bars: | |.
- |5| = 5
- |-5| = 5
- |0| = 0
Absolute value is crucial in understanding the magnitude of a signed number, regardless of its sign.
Order of Operations (PEMDAS/BODMAS)
When dealing with expressions involving signed numbers and multiple operations, the order of operations must be followed:
- Parentheses/ Brackets
- Exponents/ Orders
- Multiplication and Division (from left to right)
- Addition and Subtraction (from left to right)
Advanced Concepts and Applications
The concept of signed numbers extends far beyond basic arithmetic. Here are some advanced applications:
Vectors
Vectors are mathematical objects that possess both magnitude and direction. They are often represented using signed numbers to indicate their components along different axes. This is fundamental in physics, engineering, and computer graphics.
Complex Numbers
Complex numbers extend the concept of numbers to include an imaginary unit, denoted by 'i', where i² = -1. Complex numbers have a real part and an imaginary part, both of which can be signed numbers. They are crucial in various fields, including electrical engineering and quantum mechanics.
Matrices and Linear Algebra
Matrices are rectangular arrays of numbers, and many of these numbers are signed. Linear algebra, the study of matrices and vectors, extensively uses signed numbers in its operations and applications, such as solving systems of equations and analyzing data.
Calculus
Calculus, dealing with rates of change, relies heavily on the concept of signed numbers to represent positive and negative slopes, rates of change, and areas under curves. Understanding the sign of a derivative or an integral is critical to interpreting the results.
Financial Mathematics
In finance, signed numbers are essential for representing profits (positive) and losses (negative), assets and liabilities, and cash flow.
Practical Examples
Let's consider some real-world scenarios involving signed numbers:
Scenario 1: Bank Account
You start with $100 in your bank account. You deposit $50 and then withdraw $75. What is your final balance?
Solution: 100 + 50 - 75 = $75
Scenario 2: Temperature Change
The temperature starts at -5°C. It rises by 8°C, then drops by 3°C. What is the final temperature?
Solution: -5 + 8 - 3 = 0°C
Scenario 3: Elevation
A hiker starts at an elevation of 1500 meters. They descend 300 meters, then ascend 200 meters. What is their final elevation?
Solution: 1500 - 300 + 200 = 1400 meters
Conclusion
Signed numbers are a cornerstone of mathematics and are crucial for understanding and representing quantities with both magnitude and direction. Mastering the operations and concepts associated with signed numbers is essential for success in various mathematical and scientific fields. From basic arithmetic to advanced concepts like calculus and linear algebra, signed numbers provide a fundamental framework for modeling and solving real-world problems. Their seemingly simple nature belies their profound importance in the world of mathematics and beyond. Continued practice and application will solidify your understanding and pave the way for more advanced mathematical exploration.
Latest Posts
Latest Posts
-
What Is The Electron Configuration Of Boron
Apr 07, 2025
-
Group 17 On The Periodic Table Is Called
Apr 07, 2025
-
A Line That Intersects A Plane At A Point
Apr 07, 2025
-
3 Examples Of A Chemical Property
Apr 07, 2025
-
What Happens To Wages During A Recessionary Gap
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about What Is A Signed Number In Math . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
