What Is The Base Of A Parallelogram
Muz Play
Mar 28, 2025 · 5 min read
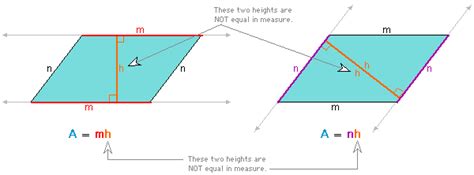
Table of Contents
What is the Base of a Parallelogram? A Comprehensive Guide
Understanding the base of a parallelogram is fundamental to grasping its area and various properties. While seemingly simple, the concept holds more depth than initially perceived. This comprehensive guide will delve into the definition, properties, and applications of the parallelogram's base, demystifying any confusion and providing a solid foundation for further geometric exploration.
Defining the Base of a Parallelogram
A parallelogram, a quadrilateral with opposite sides parallel, offers flexibility in choosing its base. Unlike triangles, where the base is typically the side resting on a horizontal plane, a parallelogram allows any of its sides to function as the base. This choice affects the calculation of the area but doesn't alter the parallelogram's fundamental properties.
Key takeaway: The base of a parallelogram is simply any chosen side of the parallelogram. There's no single "correct" base.
The Importance of Choosing a Base
While any side can serve as the base, the choice influences the calculation of the parallelogram's area. The area is determined by multiplying the base by its corresponding height. The height is the perpendicular distance between the base and the opposite side (which is parallel to the base).
Consider this: A parallelogram tilted on its side will have a different height than the same parallelogram resting on its longer side. However, the area remains the same, highlighting the interchangeability of bases.
How to Identify the Base and Height
Identifying the base is straightforward: choose any side of the parallelogram. Once the base is selected, the height is the perpendicular line segment drawn from the base to the opposite parallel side. This perpendicular distance is crucial for calculating the area.
Visualizing it: Imagine dropping a perpendicular line from a vertex of the parallelogram onto the chosen base. The length of this perpendicular line represents the height.
Properties Related to the Base
The base of a parallelogram interacts with several key properties:
-
Area: As mentioned previously, the area (A) of a parallelogram is calculated using the formula: A = base * height. This formula remains consistent regardless of the chosen base. The key is to always use the height corresponding to the chosen base.
-
Parallel Sides: The base is always parallel to its opposite side. This is the defining characteristic of a parallelogram. Therefore, selecting a base implicitly defines its parallel counterpart.
-
Midpoints: The line segment joining the midpoints of two sides of a parallelogram is always parallel to the other two sides (including the base). This property is useful in geometric proofs and constructions.
-
Symmetry: Depending on the parallelogram's type (rhombus, rectangle, square), specific symmetries exist concerning its base and height. For instance, in a square, every side can be considered a base, with the height equal to the side length.
Applications of Base Understanding
The concept of the base extends beyond simple area calculations. Understanding the base and its relationship with the height is crucial in various applications, including:
-
Engineering: Designing structures involving parallel forces, such as bridges and trusses, relies heavily on understanding parallelogram properties. The base represents a structural element, while the height influences stability and load distribution.
-
Physics: Analyzing forces and vectors often involves parallelograms. The base can represent the magnitude of a force, and the parallelogram's area might represent work done or a resultant force.
-
Computer Graphics: Parallelograms are frequently used in computer graphics to represent 2D shapes. The base and height play a role in scaling and transformation operations.
-
Cartography: The concept of parallelograms can be utilized to understand map projections and spatial relationships.
Different Types of Parallelograms and their Bases
The choice of base in special parallelograms can simplify calculations:
-
Rectangles: In a rectangle, selecting one of the longer sides as the base often leads to simpler calculations, as the height will be the shorter side. However, any side can be chosen as the base.
-
Squares: All sides of a square are equal, making any side a suitable base. The height will always equal the side length.
-
Rhombuses: In a rhombus, all sides are equal, and the choice of base doesn't affect the side length itself. However, the height will vary based on the angle between the base and the adjacent side.
-
Rhomboids: A rhomboid is a parallelogram that is neither a rhombus nor a rectangle. The choice of base will affect both the side length and the height.
Advanced Concepts and Applications
Beyond basic area calculations, the base of a parallelogram plays a significant role in more advanced geometrical concepts:
-
Vector Algebra: Parallelograms are instrumental in visualizing vector addition and subtraction. The base and adjacent side can represent two vectors, and the diagonal represents their resultant vector.
-
Coordinate Geometry: Using coordinate systems, the base and height of a parallelogram can be precisely defined by the coordinates of its vertices. This allows for precise area calculation using vector methods or determinant calculations.
-
Calculus: Parallelograms can be used to approximate the area under curves. The base represents a small interval along the x-axis, and the height represents the function's value at a particular point within that interval. This is a fundamental concept in integral calculus.
Common Misconceptions about the Base of a Parallelogram
-
Fixed Base: It's crucial to understand that a parallelogram doesn't have one fixed base. Any side can be designated as the base.
-
Height as Side Length: The height is not always the same as the side length. The height is the perpendicular distance between the base and the opposite parallel side.
-
Area Dependence on Base Selection: While the base selection changes the height, it does not change the area of the parallelogram. The area remains constant irrespective of the chosen base.
Conclusion: Mastering the Parallelogram's Base
The base of a parallelogram, while seemingly simple at first glance, plays a central role in understanding its area, properties, and diverse applications across various disciplines. By comprehending the concept of the base and its relationship with the height, you gain a solid foundation for solving geometric problems and exploring advanced mathematical concepts. Remember the flexibility in choosing a base; the choice doesn't alter the inherent properties of the parallelogram. With this understanding, you're well-equipped to tackle problems involving parallelograms with confidence and precision. The flexibility in defining the base underscores the versatility of this fundamental geometric shape.
Latest Posts
Latest Posts
-
What Is The Basic Unit Of Measurement
Mar 31, 2025
-
Is It Possible To Love 2 People At Once
Mar 31, 2025
-
What Does The Atomic Mass Of An Element Represent
Mar 31, 2025
-
Electric Field Of A Charged Disk
Mar 31, 2025
-
5 Blind Man And The Elephant
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is The Base Of A Parallelogram . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
