What Is The Domain Of Tan
Muz Play
Apr 03, 2025 · 5 min read
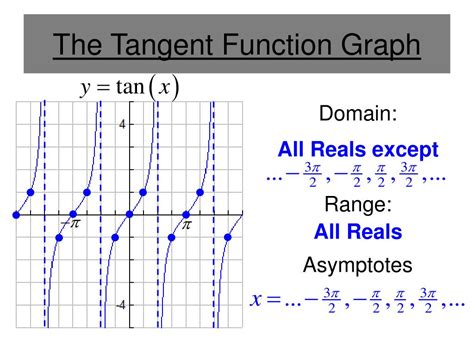
Table of Contents
What is the Domain of Tan? A Deep Dive into Trigonometric Functions
The tangent function, often abbreviated as tan(x), is a fundamental trigonometric function with a rich history and a wide range of applications in mathematics, physics, and engineering. Understanding its properties, especially its domain, is crucial for anyone working with trigonometric functions. This comprehensive guide will explore the domain of tan(x) in detail, explaining its intricacies and offering practical examples.
Understanding the Tangent Function
Before diving into the domain, let's briefly review the definition of the tangent function. In a right-angled triangle, the tangent of an angle is the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle. This can be expressed as:
tan(x) = opposite / adjacent
However, this definition only applies to acute angles (angles between 0 and 90 degrees). To extend the definition to all real numbers, we use the unit circle. On the unit circle, the tangent of an angle is the y-coordinate divided by the x-coordinate. This leads to a more general definition:
tan(x) = sin(x) / cos(x)
This definition highlights a critical point: the tangent function is undefined wherever the cosine function is equal to zero. This is because division by zero is undefined in mathematics.
Identifying Points of Undefined Tangent
The cosine function, cos(x), equals zero at certain values of x. These values are the odd multiples of π/2. In radians, this can be expressed as:
x = (2n + 1)π/2, where 'n' is any integer (..., -2, -1, 0, 1, 2, ...).
This means that the tangent function is undefined at these points. Let's illustrate this with some examples:
- n = 0: x = π/2 ≈ 1.57 radians (90 degrees)
- n = 1: x = 3π/2 ≈ 4.71 radians (270 degrees)
- n = -1: x = -π/2 ≈ -1.57 radians (-90 degrees)
At these points, the tangent function has vertical asymptotes. This means that the graph of the tangent function approaches positive or negative infinity as x approaches these values.
Defining the Domain of Tan(x)
The domain of a function represents the set of all possible input values (x-values) for which the function is defined. Since the tangent function is undefined when cos(x) = 0, we can define the domain of tan(x) as all real numbers except the odd multiples of π/2.
In set notation, the domain can be expressed as:
Domain(tan(x)) = {x ∈ ℝ | x ≠ (2n + 1)π/2, n ∈ ℤ}
This means the domain includes all real numbers except those where x is an odd multiple of π/2. The notation "∈" means "belongs to," and "ℤ" represents the set of all integers.
Visualizing the Domain: The Graph of Tan(x)
The graph of y = tan(x) visually demonstrates the domain. The graph has a repeating pattern of curves, each approaching vertical asymptotes at the points where the function is undefined. These asymptotes are located at x = π/2, 3π/2, 5π/2, and so on, and their negative counterparts. The graph never touches or crosses these vertical lines.
The periodic nature of the tangent function, with a period of π, is also clearly visible in its graph. This means that the graph repeats its pattern every π units along the x-axis.
Applications of the Tangent Function and its Domain
The tangent function and its properties, including its domain, are crucial in various applications:
1. Trigonometry and Geometry:
- Solving triangles: The tangent function is essential for solving right-angled triangles when the lengths of the opposite and adjacent sides are known, or one side and an angle are known.
- Calculating angles of elevation and depression: In surveying and navigation, the tangent function is used to determine angles of elevation or depression based on measurements of distances and heights.
- Modeling oscillations: The tangent function can model certain oscillatory phenomena, especially those with vertical asymptotes representing points of discontinuity or infinite values.
2. Calculus:
- Derivatives and integrals: The derivative and integral of the tangent function are well-defined and frequently used in calculus problems.
- Modeling rates of change: Because of its ability to model rapid changes and discontinuities, the tangent function finds applications in problems where rates of change are involved.
3. Physics and Engineering:
- Optics: The tangent function is crucial in optics for calculating angles of refraction and reflection.
- Mechanics: It helps to solve problems involving inclined planes and the analysis of forces.
- Electrical engineering: The tangent function appears in the analysis of alternating current circuits and signal processing.
4. Computer Graphics and Game Development:
- Transformations: The tangent function is involved in many geometric transformations used in computer graphics and game development, for example, in calculating rotations and projections.
Understanding the Range of Tan(x)
While we have focused primarily on the domain, understanding the range is equally important. The range of tan(x) is the set of all possible output values (y-values). Unlike the domain, which excludes specific points, the range of the tangent function encompasses all real numbers. This is because, as x approaches the asymptotes, the value of tan(x) approaches positive or negative infinity, effectively covering the entire real number line.
In set notation, the range of tan(x) is:
Range(tan(x)) = {y ∈ ℝ}
Conclusion: Mastering the Domain of Tan(x)
The domain of tan(x) is a fundamental concept in trigonometry. Understanding that the function is undefined at odd multiples of π/2 is vital for correctly applying the tangent function in various contexts. By grasping the domain, you lay a solid foundation for further exploration of trigonometric functions and their numerous applications across different fields. Remember to visualize the graph of tan(x) to solidify your understanding of its behavior and limitations. This knowledge is crucial for accurate calculations and a deeper comprehension of mathematical models in various disciplines. Mastering the domain of the tangent function will significantly enhance your mathematical proficiency and problem-solving skills.
Latest Posts
Latest Posts
-
Does Km Increase With Competitive Inhibition
Apr 03, 2025
-
Right Lateral Vs Left Lateral Fault
Apr 03, 2025
-
The Measure Of The Amount Of Matter In An Object
Apr 03, 2025
-
How To Calculate Hydronium Ion Concentration
Apr 03, 2025
-
How Many Valence Electrons Do Alkali Metals Have
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Is The Domain Of Tan . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
