What Is The Moment Of Inertia Of Particle A
Muz Play
Apr 02, 2025 · 6 min read
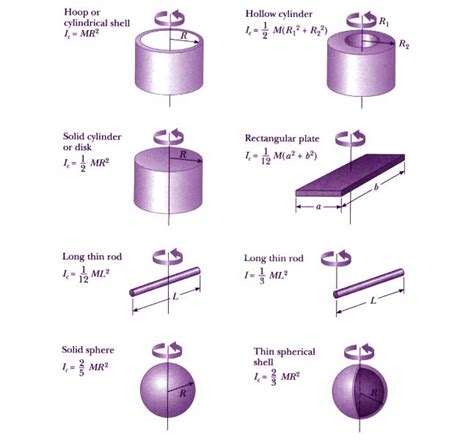
Table of Contents
What is the Moment of Inertia of Particle A? A Deep Dive into Rotational Inertia
Understanding the moment of inertia is crucial for analyzing the rotational motion of rigid bodies. This article will delve into the concept, focusing specifically on calculating the moment of inertia of a single particle, often denoted as "particle A". We'll explore the underlying principles, different approaches to calculation, and the significance of this fundamental quantity in physics and engineering.
Understanding Moment of Inertia: Resistance to Rotational Acceleration
The moment of inertia (often symbolized as I) is the rotational analog of mass in linear motion. While mass measures an object's resistance to linear acceleration, the moment of inertia quantifies an object's resistance to angular acceleration. In simpler terms, it's a measure of how difficult it is to change an object's rotational speed. A higher moment of inertia means a greater resistance to changes in rotational motion.
Think of spinning a bicycle wheel: a heavier wheel, or one with its mass distributed further from the axis of rotation, will be harder to start spinning and harder to stop. This reflects a higher moment of inertia.
Moment of Inertia of a Single Particle: The Foundation
Before tackling complex shapes, let's focus on the simplest case: a single point particle, "particle A", of mass m located at a distance r from the axis of rotation. This forms the foundation upon which the moment of inertia of more complex objects is built.
The moment of inertia of particle A is given by the equation:
I = m * r²
This equation is remarkably straightforward. It demonstrates that the moment of inertia is directly proportional to both the mass (m) of the particle and the square of its distance (r²) from the axis of rotation. This means:
- Doubling the mass doubles the moment of inertia. A heavier particle is harder to rotate.
- Doubling the distance from the axis quadruples the moment of inertia. This highlights the crucial role of the distance; mass located further from the axis significantly contributes more to the overall moment of inertia.
Illustrative Example: Calculating the Moment of Inertia of Particle A
Let's consider a concrete example. Suppose particle A has a mass of 2 kg and is located 3 meters from the axis of rotation. Using the formula above:
I = (2 kg) * (3 m)² = 18 kg·m²
Therefore, the moment of inertia of particle A is 18 kg·m². This value indicates the resistance this particle offers to rotational acceleration around the specified axis.
Extending to Multiple Particles and Rigid Bodies
The moment of inertia of a rigid body, which is an object composed of many particles, isn't simply the sum of the individual particle masses. Instead, it's the sum of the moments of inertia of all constituent particles:
I<sub>total</sub> = Σ m<sub>i</sub> * r<sub>i</sub>²
where:
- I<sub>total</sub> is the total moment of inertia of the rigid body.
- m<sub>i</sub> is the mass of the i-th particle.
- r<sub>i</sub> is the distance of the i-th particle from the axis of rotation.
- Σ denotes the summation over all particles in the body.
This summation can be challenging for complex shapes. Fortunately, integral calculus provides a powerful tool for calculating the moment of inertia of continuous mass distributions, such as rods, disks, and spheres. The general formula becomes:
I = ∫ r² dm
where:
- dm represents an infinitesimal mass element.
- The integral is taken over the entire volume of the object.
This integral calculation requires a deep understanding of calculus and often involves complex geometrical considerations. However, for many standard shapes, these integrals have already been solved, and readily available tables provide the moment of inertia values.
Significance of the Moment of Inertia in Physics and Engineering
The moment of inertia is not just a theoretical concept; it has profound implications in various fields:
1. Rotational Dynamics:
- Angular momentum: The angular momentum (L) of a rotating body is directly related to its moment of inertia and angular velocity (ω): L = Iω. This equation is fundamental in understanding rotational motion and conservation of angular momentum.
- Rotational kinetic energy: Similar to linear kinetic energy, a rotating body possesses rotational kinetic energy (KE<sub>rot</sub>), given by: KE<sub>rot</sub> = ½ Iω². This equation is crucial for analyzing the energy involved in rotational motion.
- Torque and angular acceleration: Torque (τ), the rotational equivalent of force, causes angular acceleration (α). The relationship between them is: τ = Iα. This equation demonstrates that a larger moment of inertia requires a greater torque to achieve the same angular acceleration.
2. Engineering Applications:
- Mechanical design: Engineers use moment of inertia calculations to design rotating machinery, such as flywheels, gears, and turbines. Understanding the moment of inertia helps optimize designs for efficiency, stability, and safety.
- Structural analysis: The moment of inertia is crucial in structural analysis, particularly in assessing the resistance of beams and columns to bending and twisting forces.
- Robotics: In robotics, precise control of rotational motion depends heavily on understanding and manipulating the moment of inertia of robot arms and other components.
3. Astrophysics:
- Planetary rotation: The moment of inertia of planets plays a vital role in determining their rotational dynamics, precession, and nutation.
- Stellar evolution: The moment of inertia is involved in understanding the evolution of stars, particularly their rotation rates and stability.
Parallel Axis Theorem: Shifting the Axis of Rotation
The parallel axis theorem is a powerful tool that simplifies moment of inertia calculations. It states that the moment of inertia of a rigid body about an axis parallel to its center of mass axis is equal to the moment of inertia about the center of mass axis plus the product of the mass and the square of the distance between the two axes. Mathematically:
I = I<sub>cm</sub> + Md²
Where:
- I is the moment of inertia about the parallel axis.
- I<sub>cm</sub> is the moment of inertia about the center of mass axis.
- M is the total mass of the body.
- d is the distance between the two parallel axes.
This theorem is incredibly useful because it allows us to calculate the moment of inertia about any parallel axis once the moment of inertia about the center of mass is known. This significantly simplifies calculations for many complex shapes.
Conclusion: Mastering the Moment of Inertia
Understanding the moment of inertia of a particle, and subsequently extending this knowledge to more complex systems, is fundamental to grasping rotational motion and its implications across various scientific and engineering disciplines. While the basic equation for a single particle is relatively simple, the application and extension of this concept require a solid grasp of calculus and often involve advanced mathematical techniques. However, by building a strong foundation in the fundamental principles, we can gain a profound appreciation for the significance of this crucial parameter in understanding and predicting the behavior of rotating objects. The applications, from designing efficient machinery to analyzing celestial bodies, are vast and continue to expand as our understanding deepens.
Latest Posts
Latest Posts
-
Identify All Correct Statements About The Ionization Of Water
Apr 03, 2025
-
Why Are Open Circulatory Systems Advantageous To Some Animals
Apr 03, 2025
-
Hypothesis Test For A Population Mean
Apr 03, 2025
-
Classify The Sugars As Aldoses Or Ketoses
Apr 03, 2025
-
What Is The Role Of Leukocytes During Inflammation
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about What Is The Moment Of Inertia Of Particle A . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
