What Is The Point Of Riemans Sums When Integration Exists
Muz Play
Mar 26, 2025 · 5 min read
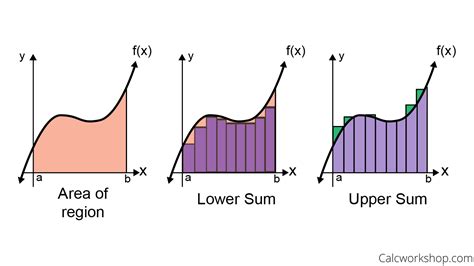
Table of Contents
What's the Point of Riemann Sums When Integration Exists?
The fundamental theorem of calculus provides a powerful and elegant way to evaluate definite integrals, rendering the seemingly laborious process of calculating Riemann sums obsolete. So, why bother learning about them at all? The answer lies in their fundamental role in understanding the very concept of integration itself. While Riemann sums might seem redundant in the face of readily available integration techniques, their pedagogical and conceptual significance remains irreplaceable. This article will explore the deeper reasons why Riemann sums are crucial, even in the presence of established integration methods.
Riemann Sums: The Foundation of Integration
Before delving into the practical applications, it's vital to grasp the foundational importance of Riemann sums. They aren't merely a cumbersome preliminary step; they're the very definition of the definite integral. The definite integral, denoted as ∫<sub>a</sub><sup>b</sup> f(x) dx, represents the signed area between the curve of a function f(x) and the x-axis, from x = a to x = b. Riemann sums provide a method to approximate this area by dividing the region into smaller rectangles and summing their areas.
Types of Riemann Sums
Several variations of Riemann sums exist, each offering a unique approach to approximating the integral:
- Left Riemann Sum: Uses the left endpoint of each subinterval to determine the height of the rectangle.
- Right Riemann Sum: Uses the right endpoint of each subinterval to determine the rectangle's height.
- Midpoint Riemann Sum: Uses the midpoint of each subinterval for the rectangle's height.
- Trapezoidal Rule: Approximates the area using trapezoids instead of rectangles, generally providing greater accuracy.
The choice of method depends on the function's behavior and the desired level of accuracy. For instance, for monotonically increasing functions, the left Riemann sum will underestimate the integral, while the right Riemann sum will overestimate it. The midpoint rule often provides a more accurate approximation than either left or right endpoint methods.
Beyond Approximation: Conceptual Understanding
While integration techniques provide precise solutions, Riemann sums offer a crucial intuitive grasp of what integration means. They visually demonstrate the process of accumulating infinitesimally small areas to obtain the total area under a curve. This visualization is invaluable for understanding the concept of limits and the connection between differentiation and integration. The fundamental theorem of calculus, while powerful, can feel abstract without the grounding provided by Riemann sums.
Visualizing the Limit Process
Riemann sums vividly illustrate the limit process central to integration. As the number of rectangles (subintervals) increases and their width decreases, the approximation gets progressively closer to the true value of the definite integral. This process highlights the concept of a limit, where the sum converges to a specific value as the number of subintervals approaches infinity. This visual representation strengthens the understanding of the rigorous mathematical definition of the definite integral.
Connecting Differentiation and Integration
The fundamental theorem of calculus establishes a profound link between differentiation and integration: the derivative of an integral is the original function (within certain constraints). While the theorem provides the mechanics, Riemann sums help visualize this connection. By examining the change in the accumulated area as the interval widens (represented by the Riemann sum), we can intuitively see the relationship between the accumulated area and its rate of change (the original function).
Riemann Sums in Numerical Integration
Even with the availability of analytical integration techniques, many real-world functions defy closed-form solutions. In such cases, numerical methods like Riemann sums become essential. While more sophisticated numerical techniques exist (like Simpson's rule and Gaussian quadrature), understanding Riemann sums forms the basis for comprehending these advanced methods.
Handling Complex Functions
Many functions encountered in scientific and engineering applications lack elementary antiderivatives. For example, consider integrating complex functions like those arising from probability distributions (e.g., the normal distribution) or those describing physical phenomena (e.g., aerodynamic forces). Riemann sums, or more advanced variations, provide a practical means to approximate the definite integrals of such functions.
Practical Applications
The applications of numerical integration using Riemann sums (or their refinements) are widespread across various fields:
- Physics: Calculating work done by a variable force, finding centers of mass, determining moments of inertia.
- Engineering: Estimating areas and volumes of irregularly shaped objects, analyzing stress distributions in structures.
- Economics: Calculating consumer surplus and producer surplus in market analysis.
- Computer Graphics: Rendering realistic images by approximating surface areas and volumes.
- Data Analysis: Approximating the area under a probability density function.
These are just a few examples illustrating the pervasive use of numerical integration in practical contexts. The foundation of these methods remains rooted in the principles underlying Riemann sums.
Beyond the Basics: Error Analysis and Refinements
The accuracy of Riemann sum approximations depends heavily on the number of subintervals used. Increasing the number of subintervals generally improves accuracy but increases computational cost. Understanding error analysis is crucial for determining the optimal number of subintervals to balance accuracy and computational efficiency.
Error Bounds and Convergence
Analyzing the error in Riemann sum approximations provides insight into the rate of convergence. Knowing the error bounds helps determine the required number of subintervals to achieve a desired level of accuracy. This is vital in numerical computations where precision matters.
Adaptive Quadrature
More advanced numerical integration techniques, like adaptive quadrature, build upon the fundamental principles of Riemann sums. Adaptive quadrature dynamically adjusts the number of subintervals based on the function's behavior, focusing more subintervals on regions where the function changes rapidly and fewer in areas where it is relatively smooth. This improves efficiency by concentrating computational resources where they are most needed.
Conclusion: An Indispensable Tool
While the fundamental theorem of calculus provides a direct route to solving many definite integrals, the importance of Riemann sums should not be underestimated. They serve as the foundational building blocks of integration, offering a concrete and visual representation of the underlying concept. Their role extends far beyond mere approximations; they provide:
- Intuitive understanding of integration: Visualizing the limit process and connecting differentiation and integration.
- Numerical tools for complex functions: Providing practical solutions when analytical methods fail.
- Basis for advanced numerical techniques: Forming the foundation for more sophisticated integration methods.
In essence, while Riemann sums might appear redundant in simple integration problems, their pedagogical and practical value remains undeniable. A thorough understanding of Riemann sums enhances the comprehension of the integral calculus, providing a strong foundation for both theoretical and applied mathematics. They are not just a stepping stone; they are an indispensable tool in the mathematician's and scientist's toolbox.
Latest Posts
Latest Posts
-
Hydrogen Is A Metal Nonmetal Or Metalloid
Mar 29, 2025
-
Equation Of Tangent Line Implicit Differentiation
Mar 29, 2025
-
According To The Bronsted Lowry Definition
Mar 29, 2025
-
What Are The Vertical Columns Called On A Periodic Table
Mar 29, 2025
-
Where Does Fermentation Take Place In A Cell
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about What Is The Point Of Riemans Sums When Integration Exists . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
