What Is The Van Der Waals Equation
Muz Play
Mar 29, 2025 · 6 min read
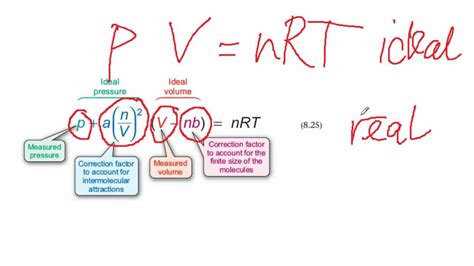
Table of Contents
What is the van der Waals Equation? A Deep Dive into Real Gas Behavior
The ideal gas law, PV = nRT, serves as a foundational concept in chemistry and physics, providing a simplified model for the behavior of gases. However, its limitations become apparent when dealing with real gases under various conditions of temperature and pressure. Real gases deviate significantly from ideal behavior, particularly at high pressures and low temperatures. This is where the van der Waals equation comes into play, offering a more accurate representation of real gas behavior by incorporating two crucial corrections: intermolecular forces and finite molecular volume.
Understanding the Limitations of the Ideal Gas Law
The ideal gas law assumes that gas molecules are point masses with negligible volume and that there are no intermolecular forces between them. These assumptions hold reasonably well at low pressures and high temperatures, where the molecules are far apart and their kinetic energy significantly outweighs the attractive forces. However, at high pressures, the volume occupied by the molecules themselves becomes a considerable fraction of the total volume, and at low temperatures, intermolecular attractive forces become significant, causing the gas to deviate from ideality.
Consequences of Ideal Gas Law Assumptions:
-
Negligible Molecular Volume: The ideal gas law treats molecules as point masses, meaning they occupy no volume. In reality, molecules have finite size, reducing the available space for movement. This leads to a smaller volume than predicted by the ideal gas law.
-
No Intermolecular Forces: The ideal gas law ignores intermolecular forces like van der Waals forces (attractive forces). These forces cause molecules to clump together, reducing the pressure exerted on the container walls compared to the ideal gas law prediction.
Introducing the van der Waals Equation: A More Realistic Model
The van der Waals equation addresses the limitations of the ideal gas law by introducing two correction factors:
-
a(Intermolecular Attraction): This constant accounts for the attractive forces between gas molecules. A higher value of 'a' indicates stronger intermolecular attraction. These forces reduce the pressure exerted by the gas. -
b(Molecular Volume): This constant accounts for the finite volume occupied by gas molecules. A higher value of 'b' indicates a larger molecular size. This reduces the available volume for the gas molecules to move in.
The van der Waals equation is expressed as:
(P + a(n/V)²)(V - nb) = nRT
Where:
- P represents the pressure of the gas.
- V represents the volume of the gas.
- n represents the number of moles of the gas.
- R represents the ideal gas constant.
- T represents the temperature of the gas.
- a represents the correction for intermolecular attractive forces.
- b represents the correction for the finite volume of gas molecules.
Interpreting the van der Waals Constants (a and b)
The constants 'a' and 'b' are specific to each gas and are determined experimentally. They reflect the unique intermolecular forces and molecular sizes of each gas.
The 'a' Constant:
-
Magnitude: A larger value of 'a' signifies stronger intermolecular attractive forces. Gases like water (H₂O) and ammonia (NH₃) with strong hydrogen bonding have significantly higher 'a' values compared to noble gases like helium (He) and neon (Ne) which have weak van der Waals forces.
-
Impact on Pressure: The term
a(n/V)²represents the reduction in pressure due to intermolecular attraction. As the concentration of gas molecules (n/V) increases, the attractive forces become more significant, leading to a greater reduction in pressure.
The 'b' Constant:
-
Magnitude: A larger value of 'b' signifies a larger molecular size. Larger molecules, such as butane (C₄H₁₀), occupy more space and have higher 'b' values than smaller molecules like methane (CH₄).
-
Impact on Volume: The term
nbrepresents the volume occupied by the gas molecules themselves. As the number of moles (n) increases, the total volume occupied by the molecules increases, leaving less free volume for the gas to expand.
Comparing the Ideal Gas Law and the van der Waals Equation
The following table summarizes the key differences between the ideal gas law and the van der Waals equation:
| Feature | Ideal Gas Law (PV = nRT) | van der Waals Equation [(P + a(n/V)²)(V - nb) = nRT] |
|---|---|---|
| Molecular Volume | Assumed negligible | Accounted for (constant 'b') |
| Intermolecular Forces | Assumed absent | Accounted for (constant 'a') |
| Applicability | Low pressure, high temperature | Wide range of pressures and temperatures |
| Accuracy | Approximate, deviates at high P, low T | More accurate, especially at high P, low T |
Applications of the van der Waals Equation
The van der Waals equation finds widespread applications in various fields:
-
Chemical Engineering: Predicting the behavior of gases in industrial processes, designing equipment, and optimizing reaction conditions.
-
Thermodynamics: Calculating thermodynamic properties of real gases, such as enthalpy, entropy, and Gibbs free energy.
-
Petroleum Engineering: Modeling the behavior of hydrocarbons in reservoirs and pipelines, crucial for oil and gas extraction.
-
Atmospheric Science: Simulating atmospheric conditions, modeling weather patterns, and understanding climate change.
-
Refrigeration and Air Conditioning: Designing refrigeration systems and predicting refrigerant behavior under various operating conditions.
Limitations of the van der Waals Equation
While the van der Waals equation represents a significant improvement over the ideal gas law, it still has limitations:
-
Simplicity: It's a relatively simple model that doesn't account for all the complexities of intermolecular interactions. More sophisticated equations of state exist for higher accuracy.
-
Critical Point Prediction: While it provides a reasonable estimate of the critical point (the temperature and pressure above which a gas cannot be liquefied), it doesn't perfectly match experimental data for all substances.
-
Specific Interactions: It doesn't explicitly account for specific types of intermolecular forces, such as hydrogen bonding, which can significantly influence gas behavior.
Beyond the van der Waals Equation: Other Equations of State
Several more complex equations of state have been developed to further refine the modeling of real gases, addressing the limitations of the van der Waals equation. These include:
-
Redlich-Kwong Equation: This equation incorporates temperature dependence into the attractive forces parameter, improving accuracy at higher temperatures.
-
Peng-Robinson Equation: This equation offers improved accuracy near the critical point and for substances with strong intermolecular forces.
-
Soave-Redlich-Kwong Equation: A modification of the Redlich-Kwong equation, often preferred for its accuracy and ease of use.
Conclusion
The van der Waals equation serves as a crucial bridge between the idealized behavior of gases described by the ideal gas law and the more complex reality of real gases. By incorporating corrections for intermolecular forces and finite molecular volume, it provides a more accurate and applicable model for a wider range of conditions. While it has limitations, its simplicity and relative accuracy have made it an essential tool in various scientific and engineering disciplines. Understanding the van der Waals equation is crucial for comprehending the behavior of real gases and their applications in numerous fields. Further advancements in the development of more sophisticated equations of state continually refine our understanding of gas behavior and enhance their predictive capabilities. The legacy of van der Waals' contribution remains a cornerstone of physical chemistry and a testament to the power of modeling in unraveling the complexities of the natural world.
Latest Posts
Latest Posts
-
Four Ways To Represent A Function
Mar 31, 2025
-
What Is The Functional Unit Of Heredity
Mar 31, 2025
-
Cracking The Code Of Life Answer Key
Mar 31, 2025
-
Delta H Is Negative Exothermic Or Endothermic
Mar 31, 2025
-
Raising And Lowering Operators Angular Momentum
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about What Is The Van Der Waals Equation . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
