Cauchy Schwarz Inequality For Complex Numbers
Muz Play
Mar 30, 2025 · 5 min read
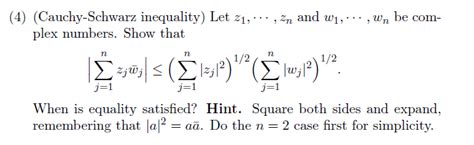
Table of Contents
Cauchy-Schwarz Inequality for Complex Numbers: A Deep Dive
The Cauchy-Schwarz inequality is a fundamental result in mathematics with far-reaching applications across various fields, including linear algebra, probability theory, and analysis. While often introduced for real numbers, its extension to complex numbers provides even greater versatility and power. This article delves into the Cauchy-Schwarz inequality for complex numbers, exploring its proof, implications, and practical applications. We'll unpack the nuances, providing a comprehensive understanding for both beginners and those seeking a deeper appreciation of this crucial inequality.
Understanding the Inequality
For complex numbers, the Cauchy-Schwarz inequality states:
For any two vectors u and v in a complex inner product space, the following inequality holds:
|⟨u, v⟩|² ≤ ⟨u, u⟩⟨v, v⟩
Where:
- ⟨u, v⟩ represents the inner product (or dot product) of vectors u and v. For complex numbers, this is defined as: ⟨u, v⟩ = Σ(uᵢ * vᵢ*), where uᵢ and vᵢ are the components of vectors u and v respectively, and vᵢ* denotes the complex conjugate of vᵢ.
- ⟨u, u⟩ and ⟨v, v⟩ represent the squared norms (lengths) of vectors u and v, respectively. They are always non-negative real numbers.
This inequality essentially bounds the magnitude of the inner product of two vectors by the product of their norms. It's a powerful tool because it provides an upper limit without requiring explicit calculation of the inner product.
Proof of the Cauchy-Schwarz Inequality for Complex Numbers
Several approaches can prove this inequality. We'll present a method that elegantly uses the properties of inner products and norms.
1. Consider a linear combination of u and v:
Let's consider a vector w defined as: w = u - λv, where λ is a complex scalar.
2. The norm of w is always non-negative:
The squared norm of w, ⟨w, w⟩, is always greater than or equal to zero:
⟨w, w⟩ = ⟨u - λv, u - λv⟩ ≥ 0
3. Expanding the inner product:
Expanding the inner product, we get:
⟨u - λv, u - λv⟩ = ⟨u, u⟩ - λ⟨v, u⟩ - λ*⟨u, v⟩ + |λ|²⟨v, v⟩ ≥ 0
4. Choosing a strategic λ:
To simplify this expression, let's choose a specific value for λ:
λ = ⟨u, v⟩ / ⟨v, v⟩ (assuming ⟨v, v⟩ ≠ 0; if ⟨v, v⟩ = 0, the inequality trivially holds)
5. Substitution and simplification:
Substituting this value of λ into the inequality and simplifying (note that ⟨v,u⟩ = ⟨u,v⟩*):
⟨u, u⟩ - (⟨u, v⟩⟨v, u⟩) / ⟨v, v⟩ - (⟨u, v⟩*⟨u, v⟩) / ⟨v, v⟩ + (|⟨u, v⟩|²/⟨v, v⟩²)⟨v, v⟩ ≥ 0
⟨u, u⟩ - (|⟨u, v⟩|²) / ⟨v, v⟩ - (|⟨u, v⟩|²) / ⟨v, v⟩ + (|⟨u, v⟩|²) / ⟨v, v⟩ ≥ 0
⟨u, u⟩ - (|⟨u, v⟩|²) / ⟨v, v⟩ ≥ 0
6. Rearrangement to obtain the Cauchy-Schwarz inequality:
Rearranging the inequality, we finally arrive at the Cauchy-Schwarz inequality for complex numbers:
|⟨u, v⟩|² ≤ ⟨u, u⟩⟨v, v⟩
Implications and Interpretations
The Cauchy-Schwarz inequality has profound geometric interpretations. In a real Euclidean space, it states that the absolute value of the dot product of two vectors is less than or equal to the product of their lengths. This translates to a statement about the angle between the two vectors:
cos²(θ) ≤ 1
Where θ is the angle between vectors u and v. The equality holds when the vectors are linearly dependent (parallel or anti-parallel).
For complex vectors, the interpretation is slightly more abstract, but the core idea remains the same: the inequality bounds the interaction between two vectors (represented by the inner product) based on their individual magnitudes (norms). Equality holds when one vector is a scalar multiple of the other.
Applications of the Cauchy-Schwarz Inequality
The Cauchy-Schwarz inequality's versatility is showcased in its widespread applications:
1. Linear Algebra:
- Bounding inner products: It provides a crucial upper bound for the inner product, which is useful in various matrix operations and analyses.
- Estimating vector norms: It can be used to estimate the norm of a vector based on its inner product with another vector.
- Proving other inequalities: It acts as a building block for proving numerous other inequalities in linear algebra.
2. Probability Theory:
- Correlation coefficient: The Cauchy-Schwarz inequality underpins the fundamental property of the correlation coefficient, which always lies between -1 and 1. This is crucial for understanding the strength and direction of relationships between random variables.
- Variance and covariance: It plays a role in establishing relationships between the variance and covariance of random variables.
3. Analysis:
- Integral inequalities: It can be extended to function spaces (using integral inner products) to derive important integral inequalities, such as the Holder inequality.
- Approximation theory: It helps bound errors in approximation techniques.
4. Quantum Mechanics:
- Quantum entanglement: Its concepts are fundamental in understanding aspects of quantum entanglement and the bounds on correlations between quantum systems.
- Quantum information theory: It finds applications in quantifying correlations in quantum information processing.
Examples and Worked Problems
Let's illustrate the Cauchy-Schwarz inequality with a few examples:
Example 1:
Let u = (1 + i, 2) and v = (3, 1 - i). Verify the Cauchy-Schwarz inequality.
- Calculate the inner product:
⟨u, v⟩ = (1 + i)(3) + (2)(1 - i) = 3 + 3i + 2 - 2i = 5 + i
- Calculate the norms:
⟨u, u⟩ = |1 + i|² + |2|² = 2 + 4 = 6 ⟨v, v⟩ = |3|² + |1 - i|² = 9 + 2 = 11
- Apply the Cauchy-Schwarz inequality:
|⟨u, v⟩|² = |5 + i|² = 26 ⟨u, u⟩⟨v, v⟩ = 6 * 11 = 66
Since 26 ≤ 66, the Cauchy-Schwarz inequality holds.
Example 2:
Consider two complex functions f(x) = x and g(x) = e^(ix) in the interval [0, 1].
The inner product can be defined as: ⟨f, g⟩ = ∫₀¹ f(x)g(x)* dx
We can apply the Cauchy-Schwarz inequality in this context to bound the integral:
|∫₀¹ xe^(-ix) dx|² ≤ (∫₀¹ x² dx)(∫₀¹ e^(ix)e^(-ix) dx)
Calculating the integrals and simplifying will demonstrate the inequality's fulfillment.
Conclusion
The Cauchy-Schwarz inequality, particularly its extension to complex numbers, is a cornerstone of numerous mathematical areas. Its elegant proof and far-reaching implications make it a crucial tool for researchers and students alike. Understanding its underlying principles and applications enhances one's grasp of many mathematical concepts and provides a powerful technique for solving various problems in diverse fields. From bounding inner products to establishing relationships between random variables and beyond, the Cauchy-Schwarz inequality continues to be a powerful and invaluable result in mathematics. This deep dive into its nuances provides a solid foundation for further exploration and application of this significant inequality.
Latest Posts
Latest Posts
-
Electric Field Lines About A Point Charge Extend
Apr 01, 2025
-
Does Ionization Energy Increase Across A Period
Apr 01, 2025
-
Integration By Parts How To Choose U And Dv
Apr 01, 2025
-
Protein Synthesis Takes Place In The
Apr 01, 2025
-
Microscopic Anatomy Of A Muscle Fiber
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Cauchy Schwarz Inequality For Complex Numbers . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
