Como Multiplicar Dos Raices Cuadradas Dividas Entre Otra Raiz Cuadrada
Muz Play
Mar 26, 2025 · 4 min read
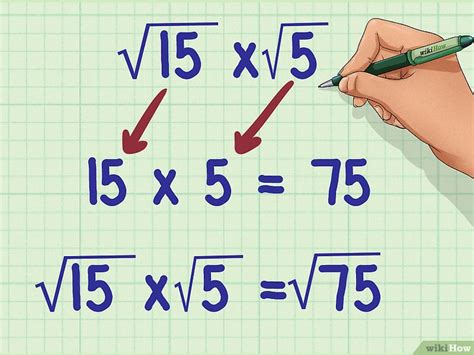
Table of Contents
How to Multiply Two Square Roots Divided by Another Square Root
Multiplying and dividing square roots can seem daunting at first, but with a systematic approach and a good understanding of the fundamental rules, it becomes a straightforward process. This comprehensive guide will walk you through the steps of multiplying two square roots and then dividing the result by another square root, explaining the underlying principles and providing numerous examples to solidify your understanding. We'll explore different scenarios and techniques to ensure you can confidently tackle any problem involving these operations.
Understanding the Basics: Properties of Square Roots
Before diving into the multiplication and division, let's review the essential properties of square roots that govern these operations.
1. The Product Rule:
The product rule states that the square root of a product is equal to the product of the square roots. Mathematically:
√(a * b) = √a * √b, where 'a' and 'b' are non-negative real numbers.
This rule is crucial because it allows us to simplify expressions involving square roots by factoring out perfect squares.
Example: √(12) = √(4 * 3) = √4 * √3 = 2√3
2. The Quotient Rule:
Similarly, the quotient rule states that the square root of a quotient is equal to the quotient of the square roots. Mathematically:
√(a / b) = √a / √b, where 'a' is a non-negative real number and 'b' is a positive real number.
This rule is equally important as it helps simplify expressions with square roots in fractions.
Example: √(9/4) = √9 / √4 = 3/2
3. Simplifying Square Roots:
Simplifying square roots involves finding the largest perfect square that is a factor of the radicand (the number inside the square root). This simplifies the expression and makes further calculations easier.
Example: √(75) = √(25 * 3) = √25 * √3 = 5√3
Multiplying Two Square Roots
The process of multiplying two square roots is a direct application of the product rule. Simply multiply the radicands together and then simplify the resulting square root.
Example 1: √2 * √8 = √(2 * 8) = √16 = 4
Example 2: √5 * √15 = √(5 * 15) = √75 = √(25 * 3) = 5√3
Example 3: √6 * √12 = √(6 * 12) = √72 = √(36 * 2) = 6√2
Example 4 (Involving Variables): √(2x) * √(8x²) = √(16x³) = √(16x² * x) = 4x√x (assuming x is non-negative)
Dividing Square Roots
Dividing square roots is similarly straightforward, utilizing the quotient rule. Divide the radicands and then simplify the resulting square root.
Example 1: √16 / √4 = √(16/4) = √4 = 2
Example 2: √18 / √2 = √(18/2) = √9 = 3
Example 3: √75 / √3 = √(75/3) = √25 = 5
Example 4 (More Complex): (√27 * √3) / √9 = √(27*3) / √9 = √81 / √9 = 9/3 = 3
Multiplying Two Square Roots and Dividing by Another
Now, let's combine the multiplication and division operations. The general approach is to first multiply the two square roots in the numerator, then divide the result by the square root in the denominator. Simplification is crucial throughout this process.
Example 1: (√6 * √10) / √5 = √(6 * 10) / √5 = √60 / √5 = √(60/5) = √12 = √(4 * 3) = 2√3
Example 2: (√2 * √18) / √3 = √(2 * 18) / √3 = √36 / √3 = 6 / √3 = (6√3) / (√3 * √3) = (6√3) / 3 = 2√3 (Rationalizing the denominator)
Example 3: (√8 * √12) / √6 = √(8 * 12) / √6 = √96 / √6 = √(96/6) = √16 = 4
Example 4 (Involving Variables): (√(2x) * √(8x²)) / √(4x) = √(16x³) / √(4x) = √(16x³/4x) = √(4x²) = 2x (assuming x is positive)
Rationalizing the Denominator
Sometimes, after the division, you might end up with a square root in the denominator. This is generally considered less elegant in mathematical expressions. To remove the square root from the denominator, a process called rationalizing the denominator is used. This involves multiplying both the numerator and the denominator by the square root in the denominator.
Example: 6 / √3 = (6 * √3) / (√3 * √3) = (6√3) / 3 = 2√3
Advanced Cases and Problem-Solving Strategies
Let's consider more complex scenarios and strategies for tackling them efficiently.
1. Expressions with Coefficients:
If the square roots have coefficients, multiply the coefficients separately and then multiply the radicands using the product rule.
Example: 2√3 * 5√6 / √2 = (25)√(36) / √2 = 10√18 / √2 = 10√(18/2) = 10√9 = 10*3 = 30
2. Nesting Square Roots:
Dealing with nested square roots requires a careful approach, often employing simplification techniques to uncover perfect squares.
Example: √(√16) = √4 = 2
3. Expressions with Variables:
Remember to handle variables with care, ensuring you understand any restrictions on their values (e.g., they must be non-negative to avoid imaginary numbers).
Example: (√x²y * √4y) / √y = √(4x²y²) / √y = √(4x²y) = 2x√y (assuming x and y are non-negative)
Conclusion
Mastering the multiplication and division of square roots is a fundamental skill in algebra and related fields. By understanding the product and quotient rules, simplifying square roots, and rationalizing the denominator, you can effectively and confidently solve a wide variety of problems involving these operations. Remember to practice regularly with different examples to build your proficiency and strengthen your mathematical intuition. The more practice you have, the more easily you will recognize patterns and apply the techniques to increasingly complex scenarios. This guide provides a strong foundation for further exploration of radical expressions and their applications in advanced mathematics.
Latest Posts
Latest Posts
-
Where Is The Bacterial Chromosome Located
Mar 29, 2025
-
Write The Chemical Formula For This Molecule
Mar 29, 2025
-
How To Calculate Velocity From Flow Rate
Mar 29, 2025
-
Write The Iupac Names Of The Given Carboxylic Acids
Mar 29, 2025
-
Multiplication Of A Polynomial By A Monomial
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Como Multiplicar Dos Raices Cuadradas Dividas Entre Otra Raiz Cuadrada . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
