Confidence Interval For Two Independent Samples Calculator
Muz Play
Mar 28, 2025 · 7 min read
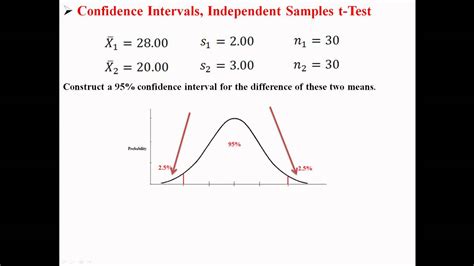
Table of Contents
Confidence Interval for Two Independent Samples Calculator: A Comprehensive Guide
Calculating confidence intervals is a cornerstone of statistical analysis, providing a range of values within which a population parameter likely falls. When comparing two independent samples, understanding how to calculate and interpret this confidence interval becomes crucial for drawing meaningful conclusions. This article will delve deep into the concept of a confidence interval for two independent samples, exploring its underlying principles, various scenarios, and practical applications. We will also guide you through the process, emphasizing interpretation and avoiding common pitfalls. While a dedicated "confidence interval for two independent samples calculator" doesn't exist as a single, universally accepted online tool, we'll provide the formulas and the rationale behind them, enabling you to perform the calculations yourself using readily available statistical software or even a spreadsheet program.
Understanding Confidence Intervals
Before diving into the specifics of two independent samples, let's solidify our understanding of confidence intervals in general. A confidence interval provides a range of plausible values for a population parameter, such as the mean or proportion, based on sample data. The level of confidence, typically expressed as a percentage (e.g., 95%, 99%), reflects the probability that the true population parameter falls within the calculated interval. A 95% confidence interval, for instance, means that if we were to repeat the sampling process many times, 95% of the calculated intervals would contain the true population parameter.
Key components of a confidence interval:
- Point Estimate: This is the best single guess for the population parameter, often the sample mean or proportion.
- Margin of Error: This accounts for the uncertainty associated with using a sample to estimate a population parameter. It's the distance between the point estimate and the upper or lower bounds of the confidence interval.
- Confidence Level: This expresses the probability that the true population parameter lies within the calculated interval.
- Critical Value: This is a value from a statistical distribution (like the t-distribution or z-distribution) that depends on the chosen confidence level and the degrees of freedom.
Confidence Interval for the Difference Between Two Independent Sample Means
This is the most common scenario when dealing with two independent samples. We aim to estimate the difference between the population means (µ1 - µ2) of two independent groups. The formula for the confidence interval depends on whether the population variances are assumed to be equal or unequal.
Case 1: Equal Variances Assumed
When we assume the population variances are equal (often tested using the F-test or Levene's test), we pool the sample variances to obtain a more precise estimate.
The formula for the confidence interval is:
(x̄₁ - x̄₂) ± t<sub>c</sub> * √[ s<sub>p</sub>² (1/n₁ + 1/n₂) ]
Where:
- x̄₁ and x̄₂: are the sample means of group 1 and group 2, respectively.
- n₁ and n₂: are the sample sizes of group 1 and group 2, respectively.
- s<sub>p</sub>²: is the pooled sample variance, calculated as:
s<sub>p</sub>² = [(n₁ - 1)s₁² + (n₂ - 1)s₂²] / (n₁ + n₂ - 2)where s₁² and s₂² are the sample variances of group 1 and group 2. - t<sub>c</sub>: is the critical t-value from the t-distribution with (n₁ + n₂ - 2) degrees of freedom at the chosen confidence level.
Case 2: Unequal Variances Assumed
If the population variances are assumed to be unequal (supported by a significant F-test or Levene's test result), we use the Welch's t-test approach, which doesn't assume equal variances.
The formula for the confidence interval is:
(x̄₁ - x̄₂) ± t<sub>c</sub> * √[ (s₁²/n₁) + (s₂²/n₂) ]
Where:
- x̄₁ and x̄₂: are the sample means of group 1 and group 2, respectively.
- n₁ and n₂: are the sample sizes of group 1 and group 2, respectively.
- s₁² and s₂²: are the sample variances of group 1 and group 2, respectively.
- t<sub>c</sub>: is the critical t-value. The degrees of freedom for the t-distribution in this case are approximated using the Welch-Satterthwaite equation, which is computationally more complex but readily handled by statistical software.
Confidence Interval for the Difference Between Two Independent Sample Proportions
When dealing with proportions (e.g., the percentage of individuals in each group exhibiting a specific characteristic), the calculation differs slightly.
The formula for the confidence interval is:
(p̂₁ - p̂₂) ± z<sub>c</sub> * √[ p̂(1-p̂)(1/n₁ + 1/n₂) ]
Where:
- p̂₁ and p̂₂: are the sample proportions of group 1 and group 2, respectively.
- n₁ and n₂: are the sample sizes of group 1 and group 2, respectively.
- p̂: is the pooled sample proportion, calculated as:
p̂ = (x₁ + x₂) / (n₁ + n₂)where x₁ and x₂ are the number of successes in group 1 and group 2. - z<sub>c</sub>: is the critical z-value from the standard normal distribution at the chosen confidence level (e.g., 1.96 for a 95% confidence level).
Interpreting the Confidence Interval
Once you've calculated the confidence interval, its interpretation is crucial. The interval provides a range of plausible values for the difference between the population parameters.
-
If the confidence interval contains zero: This suggests that there's no statistically significant difference between the two populations at the chosen confidence level. The observed difference in the samples could be due to random chance.
-
If the confidence interval does not contain zero: This indicates a statistically significant difference between the two populations. The sign of the interval tells you the direction of the difference (e.g., a positive interval suggests that the mean of group 1 is greater than the mean of group 2).
Choosing the Right Test and Assumptions
The choice between the equal variance and unequal variance t-test for comparing means hinges on whether the assumption of equal variances is met. Violating this assumption can lead to inaccurate results. Always check the assumptions of your chosen statistical test before interpreting the results.
-
Normality Assumption: While the t-test is relatively robust to violations of normality, particularly with larger sample sizes, it's advisable to check for normality using histograms, Q-Q plots, or formal normality tests (e.g., Shapiro-Wilk test). If normality is severely violated, non-parametric alternatives might be necessary (e.g., Mann-Whitney U test for comparing means).
-
Independence Assumption: The samples must be independent; observations in one group should not influence observations in the other group.
Practical Applications and Examples
Confidence intervals for two independent samples are widely used across various fields:
- Medical Research: Comparing the effectiveness of two different treatments.
- Marketing: Assessing the difference in conversion rates between two advertising campaigns.
- Education: Evaluating the impact of a new teaching method compared to a traditional one.
- Engineering: Comparing the strength of two different materials.
Example: Let's say we are comparing the average test scores of students who used a new learning app versus those who used a traditional textbook. We collect data from two independent samples and calculate the following:
- Group 1 (App): n₁ = 30, x̄₁ = 85, s₁² = 25
- Group 2 (Textbook): n₂ = 35, x̄₂ = 80, s₂² = 36
Assuming unequal variances (after conducting a Levene's test), we would use the unequal variances t-test formula to calculate the 95% confidence interval for the difference in mean scores. Using statistical software, we would obtain the interval. Let's assume the calculated interval is (2, 8). This indicates that we are 95% confident that the true difference in mean test scores between the app users and textbook users lies between 2 and 8 points, with app users scoring higher.
Using Statistical Software and Spreadsheets
While you can manually calculate confidence intervals using the formulas above, it's highly recommended to use statistical software (like R, SPSS, SAS, or Python with libraries such as SciPy and Statsmodels) or spreadsheet software (like Excel or Google Sheets) with built-in statistical functions. These tools automate the calculations, handle the complex parts (like the Welch-Satterthwaite equation), and provide more comprehensive output including p-values and other relevant statistics.
Conclusion
Calculating and interpreting confidence intervals for two independent samples is a powerful tool for making inferences about the differences between populations. Understanding the underlying principles, choosing the appropriate method based on assumptions, and utilizing statistical software are crucial for accurate and reliable results. Remember to always consider the context of your data and the limitations of statistical inference when drawing conclusions. By mastering these techniques, you can significantly enhance your ability to analyze data and make informed decisions based on evidence.
Latest Posts
Latest Posts
-
According To The Rules Of Osmosis A System Will
Mar 31, 2025
-
Where Are Chondrocytes And Osteocytes Located
Mar 31, 2025
-
List The Types Of Persuasive Speeches
Mar 31, 2025
-
The Energy Needed To Start A Chemical Reaction Is Called
Mar 31, 2025
-
Person In Environment In Social Work
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Confidence Interval For Two Independent Samples Calculator . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
