Equation Relating Electric Field And Voltage
Muz Play
Mar 31, 2025 · 6 min read
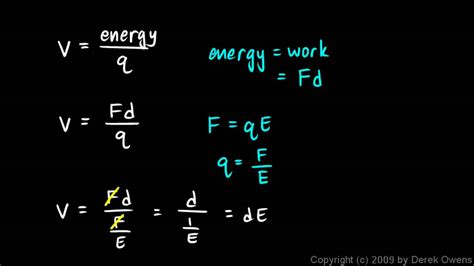
Table of Contents
The Equation Relating Electric Field and Voltage: A Deep Dive
The relationship between electric field and voltage is fundamental to understanding electromagnetism. While seemingly simple at first glance, a thorough understanding requires delving into the nuances of both concepts and their interconnectedness. This article will explore the equation linking electric field and voltage, examining its derivation, applications, and limitations. We'll also explore various scenarios and provide practical examples to solidify your grasp of this crucial concept.
Understanding Electric Field and Voltage
Before diving into the equation, let's establish a clear understanding of the individual components: electric field and voltage (or potential difference).
Electric Field: A Force Field
The electric field, denoted by E, is a vector field that describes the force experienced by a unit positive charge at any given point in space. Imagine it as an invisible influence that permeates space around charged objects. The strength and direction of the field are determined by the distribution and magnitude of the charges creating it. A stronger charge will create a stronger electric field, and the field lines will point away from positive charges and towards negative charges. The units of electric field are Newtons per Coulomb (N/C) or Volts per meter (V/m).
Voltage: Potential Energy Difference
Voltage, also known as electric potential difference, represents the work done per unit charge in moving a charge between two points in an electric field. It's a scalar quantity, meaning it only has magnitude, not direction. It describes the potential energy difference between two locations. A higher voltage indicates a greater potential energy difference, meaning more work is required to move a charge between those points. The units of voltage are Volts (V).
Deriving the Equation: Electric Field from Voltage
The relationship between the electric field E and voltage V is most clearly seen in a uniform electric field. In such a field, the field lines are parallel and equally spaced. Consider two points, A and B, separated by a distance 'd' in a uniform electric field. The voltage difference (V) between these points is given by:
V = E * d
Where:
- V is the voltage difference between points A and B (in Volts).
- E is the magnitude of the uniform electric field (in V/m).
- d is the distance between points A and B (in meters), measured along the direction of the electric field.
This equation tells us that the voltage difference between two points is directly proportional to the electric field strength and the distance between the points. A stronger electric field or a larger separation will result in a greater voltage difference.
Derivation from Work and Energy
This equation can be derived from the definition of voltage as the work done per unit charge. The work (W) done in moving a charge 'q' through a distance 'd' in a uniform electric field is given by:
W = F * d
where F is the force on the charge, given by:
F = q * E
Substituting this into the work equation, we get:
W = q * E * d
Voltage (V) is defined as the work done per unit charge:
V = W / q
Therefore:
V = (q * E * d) / q
Simplifying, we obtain the fundamental equation:
V = E * d
Applications of the Equation: From Capacitors to Electrophysiology
The equation V = E * d has widespread applications across various fields of physics and engineering. Here are some notable examples:
1. Capacitors:
Capacitors store electrical energy by accumulating charge on two conductive plates separated by an insulator (dielectric). The electric field within the capacitor is uniform (assuming ideal conditions), and the voltage across the capacitor is directly related to the electric field strength and the separation between the plates. Understanding this relationship is crucial for designing and analyzing capacitor circuits.
2. Electrophysiology:
In biology and medicine, this equation is vital for understanding the electric fields and potential differences across cell membranes. The movement of ions across these membranes creates electric fields and potential differences essential for nerve impulse transmission and muscle contraction. Analyzing these processes often involves applying this fundamental equation to model the behavior of biological systems.
3. High Voltage Engineering:
In high-voltage applications, such as power transmission lines, understanding the relationship between electric field and voltage is crucial for preventing electrical breakdown (dielectric breakdown) of the insulating materials. By carefully controlling the electric field strength, engineers can ensure the safe and reliable operation of high-voltage equipment.
4. Vacuum Tubes and Other Devices:
The electric field within vacuum tubes governs the motion of electrons and ions. Understanding the voltage and its relationship to the electric field is vital for analyzing the behavior of electron beams and other phenomena in these devices.
Beyond Uniform Fields: More Complex Scenarios
The equation V = E * d is strictly valid only for uniform electric fields. In non-uniform fields, the electric field strength varies across space. In such situations, we need to use integral calculus to find the relationship between voltage and electric field. The voltage difference between two points A and B is given by the line integral:
V = - ∫<sub>A</sub><sup>B</sup> E • dl
Where:
- E is the electric field vector.
- dl is an infinitesimal displacement vector along the path from A to B.
- The integral is a line integral along the chosen path from A to B. The negative sign indicates that the voltage decreases in the direction of the electric field.
This equation is more general and can be applied to any electric field, whether uniform or not. The line integral accounts for the variations in the electric field along the chosen path.
Limitations and Considerations
While the equation V = Ed provides a useful approximation in many cases, it's crucial to acknowledge its limitations:
- Uniform Field Assumption: The equation only holds true for perfectly uniform electric fields. In reality, perfectly uniform fields are rare.
- Idealized Conditions: The equation assumes the absence of other physical effects, such as polarization or conductivity in the surrounding medium. These effects can influence the electric field and voltage relationship.
- Path Dependence (Non-Uniform Fields): In non-uniform fields, the voltage difference between two points depends on the chosen path between them, highlighting the importance of the line integral formulation.
Conclusion: A cornerstone concept in Electromagnetism
The relationship between electric field and voltage, represented by the equation V = E * d (for uniform fields) or its more general integral form, is a cornerstone of electromagnetism. Understanding this relationship is critical for analyzing a wide range of phenomena, from the operation of capacitors and high-voltage systems to the intricacies of biological processes. While the simplified equation provides a helpful starting point, grasping its limitations and the more general integral approach is crucial for tackling complex scenarios involving non-uniform electric fields. This deep understanding of the electric field and voltage relationship forms a robust foundation for further exploration in the vast field of electromagnetism and its numerous applications. By continually building upon this base, you can unlock a more profound comprehension of the electromagnetic forces shaping our world.
Latest Posts
Latest Posts
-
Examples Of Instantaneous Rate Of Change
Apr 01, 2025
-
How Is The Use Of Symbols Related To Culture
Apr 01, 2025
-
As You Move Across The Periodic Table
Apr 01, 2025
-
What Is In The Atmosphere Of Jupiter
Apr 01, 2025
-
What Does A Negative Reduction Potential Mean
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Equation Relating Electric Field And Voltage . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
