Express The Inequality Using Interval Notation
Muz Play
Apr 01, 2025 · 6 min read
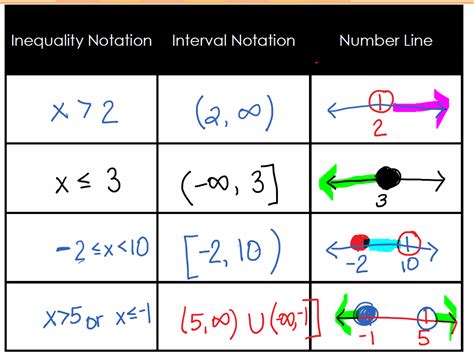
Table of Contents
Expressing Inequalities Using Interval Notation: A Comprehensive Guide
Interval notation is a concise and efficient way to represent sets of numbers, particularly those defined by inequalities. Understanding interval notation is crucial for anyone working with mathematics, especially in fields like calculus, algebra, and data analysis. This comprehensive guide will delve into the intricacies of interval notation, explaining its various forms, how to express inequalities using this notation, and offering practical examples to solidify your understanding.
Understanding the Fundamentals of Interval Notation
Interval notation uses brackets and parentheses to define a range of values. The type of bracket used signifies whether the endpoints are included or excluded from the interval.
-
Parentheses
(and): These indicate that the endpoint is not included in the interval. This is used for inequalities involving<(less than) and>(greater than). -
Brackets
[and]: These indicate that the endpoint is included in the interval. This is used for inequalities involving≤(less than or equal to) and≥(greater than or equal to). -
Infinity
∞and Negative Infinity-∞: These symbols represent unbounded intervals. Infinity is always associated with a parenthesis, as it is not a specific number that can be included in the interval.
Expressing Different Types of Inequalities in Interval Notation
Let's break down how to express various types of inequalities using interval notation:
1. Inequalities with One Variable
These are the most basic forms of inequalities. Let's consider examples involving the variable x:
-
x > a: This inequality means x is greater than a. In interval notation, this is expressed as (a, ∞). Note the parenthesis because a is not included, and the infinity symbol always uses a parenthesis.
-
x ≥ a: This inequality means x is greater than or equal to a. In interval notation, this is expressed as [a, ∞). The bracket indicates that a is included.
-
x < a: This inequality means x is less than a. In interval notation, this is expressed as (-∞, a). Both endpoints use parentheses.
-
x ≤ a: This inequality means x is less than or equal to a. In interval notation, this is expressed as (-∞, a]. The bracket indicates that a is included.
Examples:
- x > 3: (3, ∞)
- x ≥ -2: [-2, ∞)
- x < 5: (-∞, 5)
- x ≤ 0: (-∞, 0]
2. Compound Inequalities
Compound inequalities involve two or more inequalities combined. Let's explore the common types:
-
a < x < b: This means x is greater than a and less than b. In interval notation, this is expressed as (a, b). Both endpoints are excluded.
-
a ≤ x < b: This means x is greater than or equal to a and less than b. In interval notation, this is expressed as [a, b). a is included, but b is excluded.
-
a < x ≤ b: This means x is greater than a and less than or equal to b. In interval notation, this is expressed as (a, b]. a is excluded, but b is included.
-
a ≤ x ≤ b: This means x is greater than or equal to a and less than or equal to b. In interval notation, this is expressed as [a, b]. Both endpoints are included.
Examples:
- -1 < x < 4: (-1, 4)
- 2 ≤ x < 7: [2, 7)
- -5 < x ≤ 0: (-5, 0]
- 0 ≤ x ≤ 10: [0, 10]
3. Unions and Intersections of Intervals
When dealing with multiple intervals, we use union (∪) and intersection (∩) symbols.
-
Union (∪): This combines all values from both intervals. It represents the "or" condition.
-
Intersection (∩): This represents the values that are common to both intervals. It represents the "and" condition.
Examples:
Let's say we have two intervals: A = (-∞, 2) and B = [3, ∞)
-
A ∪ B: This represents the union of A and B, which is (-∞, 2) ∪ [3, ∞). This means x is either less than 2 or greater than or equal to 3.
-
A ∩ B: This represents the intersection of A and B, which is an empty set, denoted as ∅ or {}. There are no values common to both intervals.
Let's consider another example: C = (1, 5) and D = [3, 7]
-
C ∪ D: This is (1, 7]. It combines all values from both intervals.
-
C ∩ D: This is [3, 5). It represents the overlap between the two intervals.
Solving Inequalities and Expressing Solutions in Interval Notation
Solving inequalities often involves manipulating the inequality to isolate the variable. The solution is then expressed using interval notation.
Example:
Solve the inequality 2x + 5 < 11 and express the solution in interval notation.
- Subtract 5 from both sides: 2x < 6
- Divide both sides by 2: x < 3
The solution in interval notation is (-∞, 3).
Example with Compound Inequality:
Solve the inequality -3 ≤ 4x - 7 ≤ 5 and express the solution in interval notation.
- Add 7 to all parts of the inequality: 4 ≤ 4x ≤ 12
- Divide all parts by 4: 1 ≤ x ≤ 3
The solution in interval notation is [1, 3].
Advanced Applications and Considerations
Interval notation is a fundamental tool in more advanced mathematical concepts:
-
Calculus: Interval notation is extensively used to define domains and ranges of functions, intervals of convergence for series, and intervals where functions are increasing or decreasing.
-
Real Analysis: Interval notation is essential for defining open and closed sets, understanding continuity, and working with limits.
-
Linear Programming: Interval notation can help define feasible regions in optimization problems.
-
Data Analysis: Intervals are used in defining ranges of data values, creating histograms, and analyzing distributions.
Common Mistakes to Avoid
-
Confusing parentheses and brackets: Carefully consider whether the endpoints are included or excluded.
-
Incorrect use of infinity: Remember that infinity is always paired with a parenthesis.
-
Forgetting the union or intersection symbol: Use the appropriate symbol (∪ or ∩) when combining multiple intervals.
-
Not simplifying the interval: Always aim to express the interval in its simplest form. For example, (-∞, 2) ∪ (2, ∞) can be simplified to (-∞, 2) ∪ (2, ∞), but this is not equivalent to (-∞, ∞) because it excludes the value 2 itself.
By paying attention to these details, you can master the use of interval notation and apply it confidently across various mathematical contexts.
Conclusion
Interval notation is a powerful tool for representing sets of numbers defined by inequalities. By understanding the different types of brackets and how they relate to inclusion and exclusion of endpoints, you can effectively express inequalities in a concise and unambiguous way. This guide provides a solid foundation for understanding and applying interval notation in various mathematical and data analysis applications. Remember to practice regularly, and you'll find this notation becomes second nature. Mastering interval notation will significantly enhance your ability to work with inequalities and contribute to a deeper understanding of many mathematical concepts.
Latest Posts
Latest Posts
-
Skewed Left Stem And Leaf Plot
Apr 02, 2025
-
Molecules Consisting Only Of Carbon And Hydrogen Are Called
Apr 02, 2025
-
How To Read A Solubility Curve
Apr 02, 2025
-
Difference Between Fractional And Simple Distillation
Apr 02, 2025
-
What Are The Components Of A Language
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Express The Inequality Using Interval Notation . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
