Express The Interval As An Inequality
Muz Play
Apr 02, 2025 · 6 min read
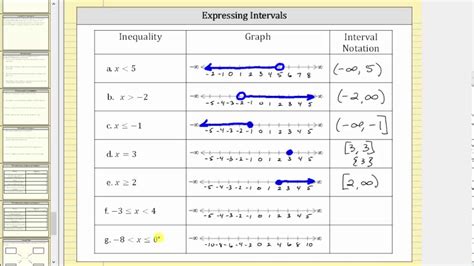
Table of Contents
Expressing Intervals as Inequalities: A Comprehensive Guide
Understanding how to express intervals as inequalities is a fundamental skill in mathematics, particularly in algebra and calculus. It's crucial for accurately representing sets of numbers and solving problems involving ranges and domains of functions. This comprehensive guide will delve into the various types of intervals, how to convert them into inequalities, and provide numerous examples to solidify your understanding. We'll also explore the nuances of using brackets and parentheses to denote inclusion and exclusion of endpoints.
Types of Intervals
Before diving into the conversion process, let's review the different types of intervals:
1. Open Interval
An open interval excludes its endpoints. It's represented using parentheses ( ). For example, the open interval (a, b) represents all real numbers x such that a < x < b. Neither a nor b is included in the set.
2. Closed Interval
A closed interval includes both its endpoints. It's denoted using square brackets [ ]. For example, the closed interval [a, b] represents all real numbers x such that a ≤ x ≤ b. Both a and b are included in the set.
3. Half-Open Intervals
Half-open intervals include one endpoint but exclude the other. There are two types:
- (a, b]: This represents all real numbers x such that a < x ≤ b. a is excluded, and b is included.
- [a, b): This represents all real numbers x such that a ≤ x < b. a is included, and b is excluded.
Converting Intervals to Inequalities
The process of converting an interval to an inequality is straightforward. The key is to understand the meaning of the brackets and parentheses and to translate that meaning into the appropriate inequality symbols.
Rule:
- Parentheses
(or): Translate to the strict inequality symbols<or>. - Brackets
[or]: Translate to the inclusive inequality symbols ≤ or ≥.
Examples:
- (2, 5): This translates to the inequality 2 < x < 5. x is greater than 2 and less than 5.
- [-1, 3]: This translates to the inequality -1 ≤ x ≤ 3. x is greater than or equal to -1 and less than or equal to 3.
- (-∞, 7): This represents all real numbers less than 7. The inequality is x < 7. Note that ∞ (infinity) is always used with a parenthesis because infinity is not a number, it represents an unbounded range.
- [4, ∞): This represents all real numbers greater than or equal to 4. The inequality is x ≥ 4. Again, ∞ is always paired with a parenthesis.
- (-3, 0]: This translates to -3 < x ≤ 0. x is greater than -3 and less than or equal to 0.
- [-π, π): This represents -π ≤ x < π.
Infinite Intervals and Their Inequalities
Infinite intervals represent unbounded sets of numbers extending to positive or negative infinity. Remember that infinity is not a number; it's a concept representing an unbounded range. Therefore, infinity is always paired with a parenthesis.
Examples:
- (-∞, ∞): This represents all real numbers. The inequality is -∞ < x < ∞, or simply stated as x ∈ ℝ (x belongs to the set of real numbers).
- (-∞, a]: This represents all real numbers less than or equal to 'a'. The inequality is x ≤ a.
- [a, ∞): This represents all real numbers greater than or equal to 'a'. The inequality is x ≥ a.
- (a, ∞): This represents all real numbers greater than 'a'. The inequality is x > a.
- (-∞, a): This represents all real numbers less than 'a'. The inequality is x < a.
Compound Inequalities
Sometimes, you'll encounter intervals that need to be expressed using compound inequalities. These inequalities combine multiple inequalities to describe a more complex range. Let's look at some examples:
-
The union of two intervals: Suppose you have the intervals (-∞, 2) and [5, ∞). The union of these intervals represents all real numbers less than 2 or greater than or equal to 5. The inequality would be x < 2 or x ≥ 5.
-
The intersection of two intervals: Consider the intervals [1, 7] and [3, 10]. The intersection of these intervals represents the numbers that are in both intervals. This corresponds to the interval [3, 7], and the inequality is 3 ≤ x ≤ 7.
Solving Inequalities Involving Intervals
Understanding intervals is not just about representation; it's also crucial for solving inequalities. Let’s look at a few examples:
Example 1: Solve the inequality 2x + 1 < 7.
- Subtract 1 from both sides: 2x < 6
- Divide both sides by 2: x < 3
The solution is the interval (-∞, 3).
Example 2: Solve the inequality -3 ≤ 4x - 5 ≤ 9.
- Add 5 to all parts of the inequality: 2 ≤ 4x ≤ 14
- Divide all parts by 4: 0.5 ≤ x ≤ 3.5
The solution is the interval [0.5, 3.5].
Example 3: Solve the inequality |x - 2| < 3.
Recall that the inequality |a| < b is equivalent to -b < a < b. Therefore:
-3 < x - 2 < 3 Add 2 to all parts: -1 < x < 5
The solution is the interval (-1, 5).
Practical Applications
The ability to express intervals as inequalities is essential in numerous mathematical and real-world applications:
-
Domain and Range of Functions: Finding the domain and range of a function often involves expressing these sets using inequalities derived from interval notation. For example, if the domain of a function is given as (0, ∞), this means the function is defined only for positive real numbers.
-
Calculus: Intervals are crucial in defining limits, derivatives, and integrals. Understanding interval notation and inequalities is fundamental to understanding these core calculus concepts.
-
Statistics: In statistics, intervals are used to represent confidence intervals and other statistical measures. These intervals provide a range of values within which a parameter or statistic is likely to fall.
-
Real-World Scenarios: Intervals are used extensively in various real-world scenarios. For instance, expressing the acceptable temperature range of a refrigerator, the allowable weight limits for an elevator, or the appropriate dosage range of a medication might all use intervals.
Advanced Topics and Further Exploration
This comprehensive guide provided a solid foundation in understanding intervals and inequalities. However, to deepen your understanding, consider exploring further topics such as:
-
Interval Arithmetic: This involves performing arithmetic operations (addition, subtraction, multiplication, division) on intervals.
-
Set Theory and Intervals: Intervals can be rigorously defined within the framework of set theory, providing a more formal mathematical treatment.
By mastering the relationship between intervals and inequalities, you will significantly improve your mathematical skills and your ability to effectively represent and manipulate numerical data and ranges. Remember to pay close attention to the inclusion or exclusion of endpoints, always using brackets and parentheses correctly to ensure accurate representation. Practice diligently with diverse examples to solidify your understanding and become proficient in this crucial mathematical concept.
Latest Posts
Latest Posts
-
Interpreting Data Absorption Spectra And Photosynthetic Pigments
Apr 03, 2025
-
Where Are The Cell Bodies For The Sensory Neurons Located
Apr 03, 2025
-
Difference Between Amorphous Solid And Crystalline Solid
Apr 03, 2025
-
Alkali Metals Alkaline Earth Metals Halogens And Noble Gases
Apr 03, 2025
-
What Determines Primary Structure Of A Protein
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Express The Interval As An Inequality . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
