Factoring Trinomials With A Leading Coefficient
Muz Play
Mar 31, 2025 · 6 min read
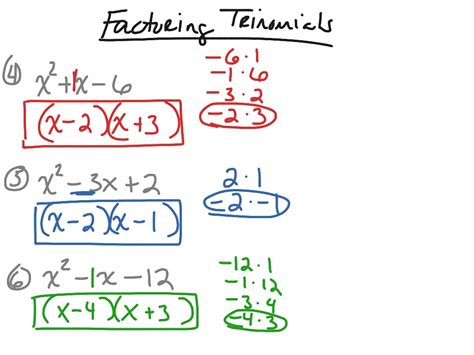
Table of Contents
Factoring Trinomials with a Leading Coefficient: A Comprehensive Guide
Factoring trinomials is a fundamental skill in algebra, crucial for solving quadratic equations and simplifying algebraic expressions. While factoring simple trinomials (where the leading coefficient is 1) is relatively straightforward, factoring trinomials with a leading coefficient greater than 1 requires a more systematic approach. This comprehensive guide will equip you with the knowledge and techniques to master this essential algebraic skill.
Understanding Trinomials and Leading Coefficients
A trinomial is a polynomial with three terms. A general trinomial can be expressed in the form:
ax² + bx + c
where 'a', 'b', and 'c' are constants, and 'a' is the leading coefficient. When 'a' is equal to 1, factoring is simpler. However, when 'a' is greater than 1, the factoring process becomes more complex, demanding a more sophisticated strategy.
Methods for Factoring Trinomials with a Leading Coefficient
Several methods exist for factoring trinomials with a leading coefficient greater than 1. We'll explore two of the most common and effective approaches: the AC method and the grouping method.
1. The AC Method (also known as the Product-Sum method)
The AC method leverages the relationship between the product and sum of the factors of the leading and constant terms. Here's a step-by-step guide:
Step 1: Find the product 'ac'.
Multiply the leading coefficient (a) by the constant term (c). This product is crucial for identifying the appropriate factors.
Step 2: Find two numbers that multiply to 'ac' and add up to 'b'.
This is the core of the AC method. You need to find two numbers whose product equals 'ac' and whose sum equals the coefficient of the middle term ('b'). This might require some trial and error, especially with larger numbers.
Step 3: Rewrite the middle term ('bx') using the two numbers found in Step 2.
Rewrite the original trinomial, splitting the middle term into two terms using the two numbers you found.
Step 4: Factor by grouping.
Group the first two terms and the last two terms together. Factor out the greatest common factor (GCF) from each group. You should now have a common binomial factor.
Step 5: Factor out the common binomial factor.
Factor out the common binomial expression to obtain the fully factored form of the trinomial.
Example:
Let's factor the trinomial 6x² + 11x + 4.
- ac = 6 * 4 = 24
- Two numbers that multiply to 24 and add to 11 are 8 and 3.
- Rewrite the middle term: 6x² + 8x + 3x + 4
- Factor by grouping: 2x(3x + 4) + 1(3x + 4)
- Factor out the common binomial factor: (2x + 1)(3x + 4)
Therefore, the factored form of 6x² + 11x + 4 is (2x + 1)(3x + 4).
2. The Grouping Method (for Trinomials easily factorable by inspection)
While the AC method is systematic, some trinomials lend themselves to a more intuitive approach – the grouping method. This method is particularly useful when you can quickly identify the factors by inspection.
Step 1: Identify potential binomial factors.
Look for two binomials whose product will yield the original trinomial. This involves considering the factors of the leading coefficient ('a') and the constant term ('c').
Step 2: Check your factors using FOIL.
After selecting potential binomial factors, use the FOIL method (First, Outer, Inner, Last) to expand the binomials and verify that the result matches the original trinomial.
Step 3: Adjust factors as needed.
If your initial guess doesn't match, adjust the factors until you achieve the correct result. This often requires some trial and error.
Example:
Let's factor the trinomial 2x² + 7x + 3.
By inspection, you might realize that (2x + 1)(x + 3) could be the factored form.
Using FOIL: (2x + 1)(x + 3) = 2x² + 6x + x + 3 = 2x² + 7x + 3.
The factors are correct. Therefore, the factored form of 2x² + 7x + 3 is (2x + 1)(x + 3).
Advanced Techniques and Considerations
-
Factoring out a Greatest Common Factor (GCF): Always begin by factoring out the GCF of all the terms in the trinomial. This simplifies the subsequent factoring process.
-
Difference of Squares: Remember that a difference of squares (a² - b²) can be factored as (a + b)(a - b). This can sometimes be applied as part of a larger factoring problem.
-
Perfect Square Trinomials: A perfect square trinomial is of the form (ax + b)², which expands to a²x² + 2abx + b². Recognizing perfect square trinomials can save you time.
-
Handling Negative Coefficients: When dealing with negative coefficients, pay close attention to the signs when applying the AC method or choosing binomial factors.
-
Prime Trinomials: Some trinomials cannot be factored using integer coefficients. These are called prime trinomials.
Troubleshooting Common Mistakes
-
Incorrectly identifying factors in the AC method: Double-check your calculations when finding factors that multiply to 'ac' and add to 'b'.
-
Errors in grouping: Ensure that you correctly factor out the GCF from each group in the grouping method.
-
Incorrect sign assignment: Pay close attention to the signs of the terms within the binomial factors. A single incorrect sign will result in an incorrect factored form.
-
Forgetting to check your answer: Always expand your factored form using FOIL to verify that it correctly yields the original trinomial.
Practical Applications and Real-World Relevance
Factoring trinomials isn't just an abstract algebraic exercise; it has significant applications in various fields:
-
Solving Quadratic Equations: Factoring is a key method for solving quadratic equations, enabling you to find the roots or zeros of the equation. This is fundamental in physics, engineering, and economics, where quadratic equations model numerous phenomena.
-
Graphing Quadratic Functions: The factored form of a quadratic equation reveals the x-intercepts of its graph, providing essential information about the parabola's shape and location.
-
Calculus: Factoring simplifies many calculus operations, particularly in integration and differentiation.
-
Computer Programming: Factoring algorithms are used in computer science for various computational tasks, including optimization and code simplification.
Conclusion
Mastering the art of factoring trinomials with a leading coefficient is a critical step towards advanced algebraic proficiency. By consistently applying the AC method or the grouping method, carefully managing signs, and verifying your results, you can confidently tackle even the most challenging trinomial factoring problems. Remember to always start by looking for a greatest common factor and to check your work. Practice is key to developing fluency and speed in this essential algebraic skill. The more you practice, the more readily you will recognize patterns and efficiently determine the correct factors. With dedication and persistent effort, factoring trinomials will become second nature, opening up a world of more advanced mathematical concepts.
Latest Posts
Latest Posts
-
How To Find Moles Of Naoh Used In Titration
Apr 02, 2025
-
Different Conformations Of The Same Compound
Apr 02, 2025
-
Induced Fit Model Vs Lock And Key
Apr 02, 2025
-
Colligative Properties Freezing Point Depression Lab
Apr 02, 2025
-
Matrix As A Product Of Elementary Matrices
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Factoring Trinomials With A Leading Coefficient . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
